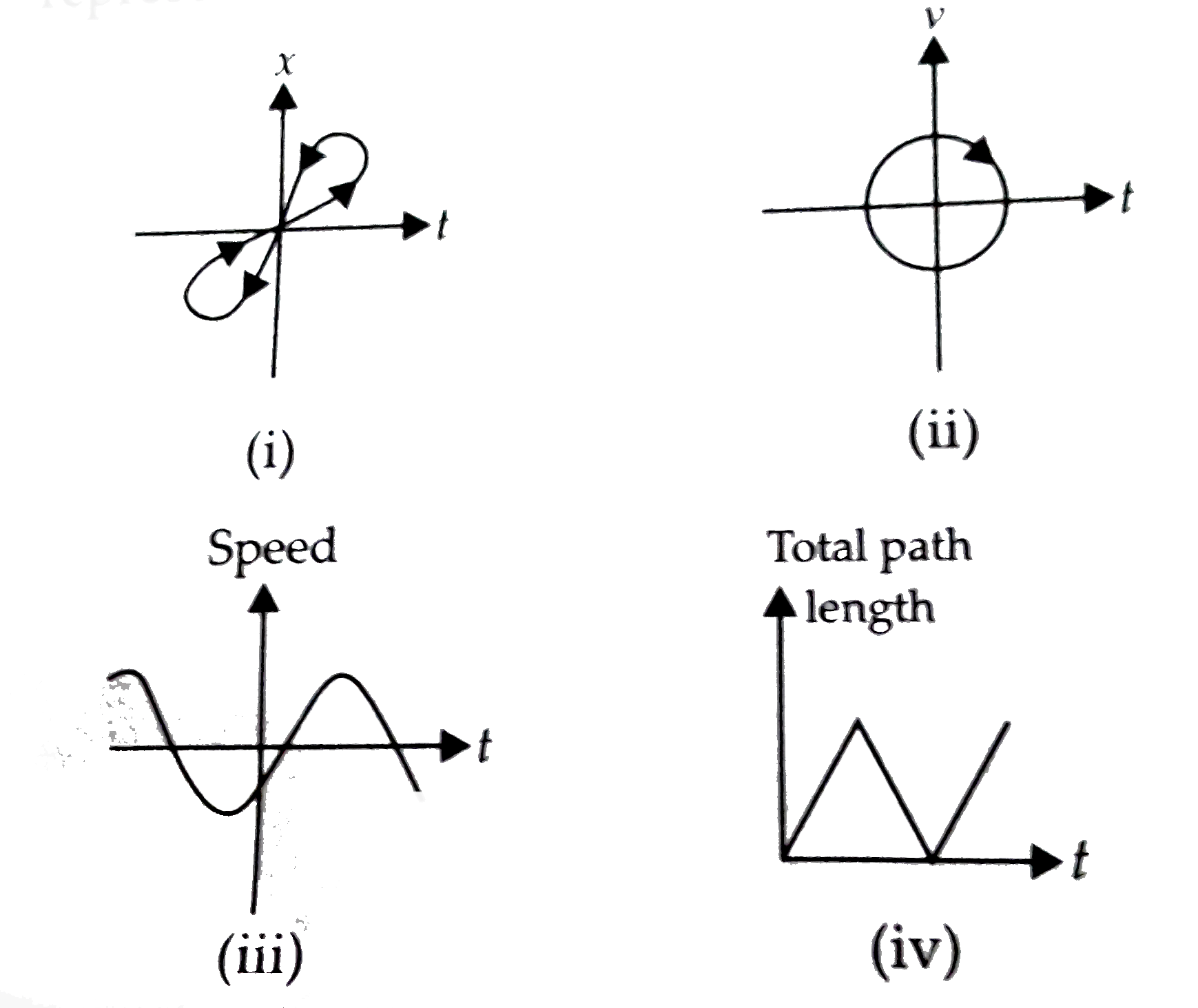
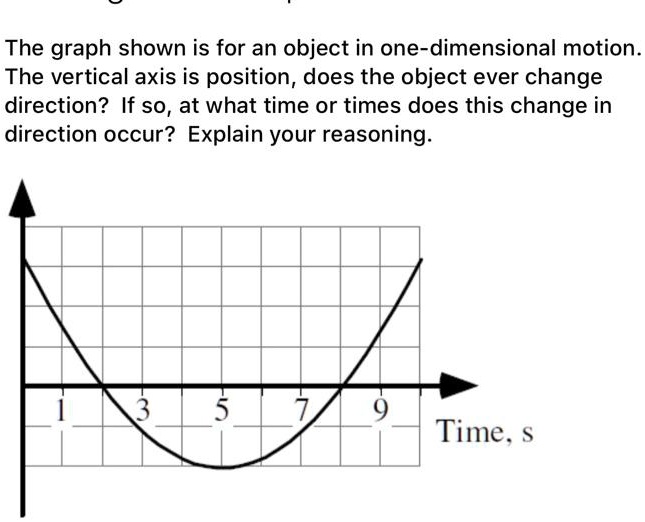
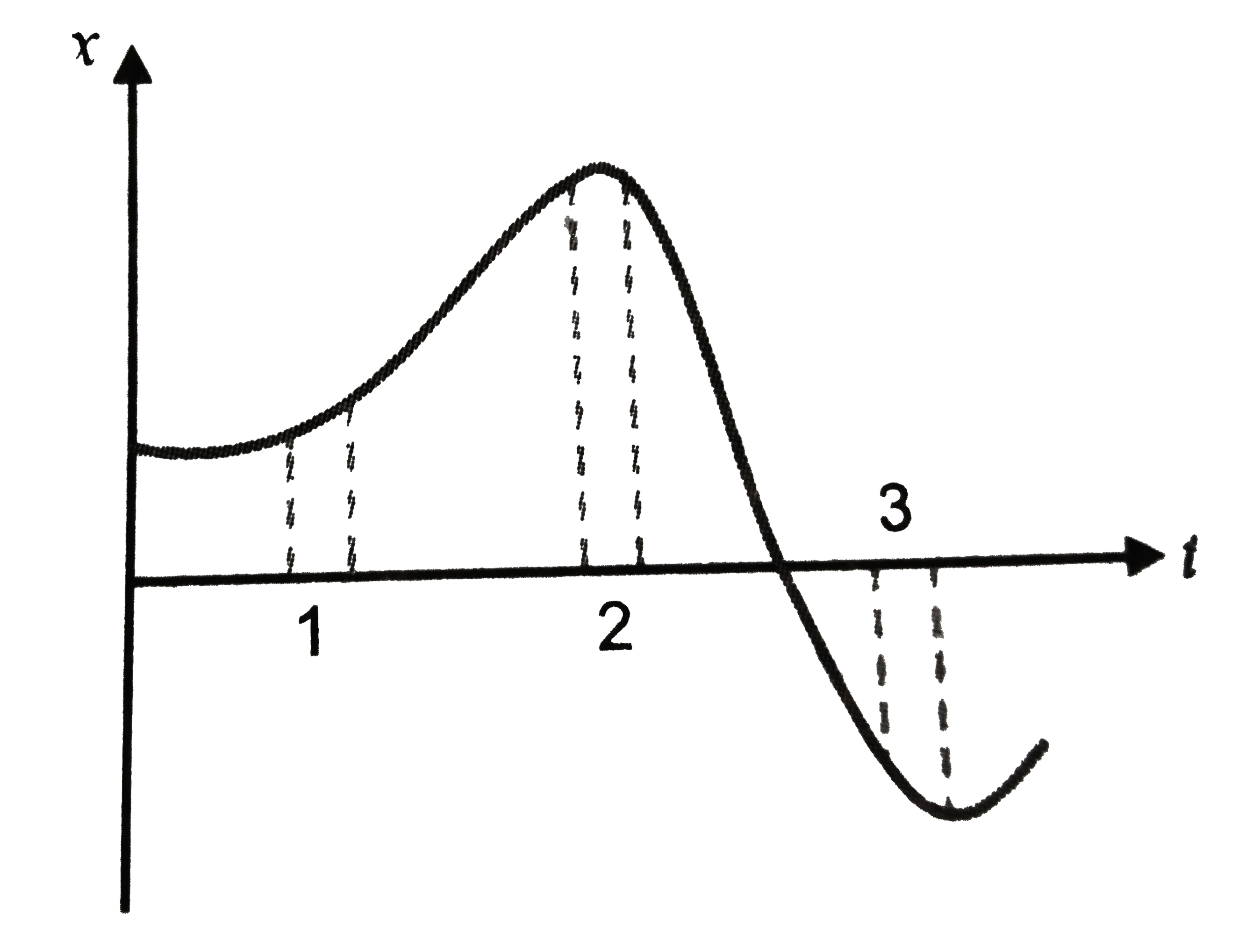
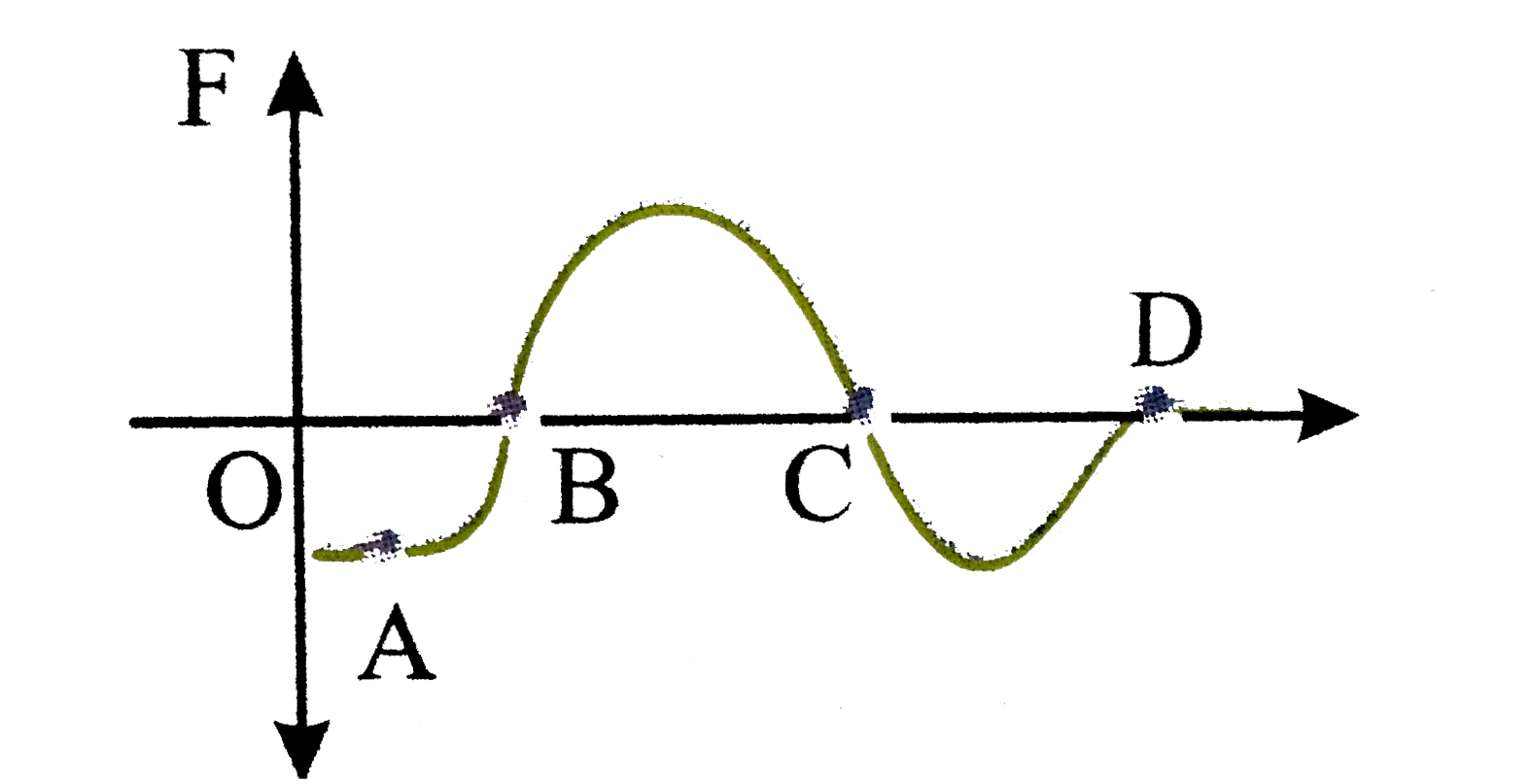
What Everybody Ought To Know About Is A Curve One-dimensional Box Area Chart

One says that the curve is defined over f.

Is a curve one-dimensional. Distance from an end point or. The scheme x = spec(k[x, y]/(f)) is a curve if. A straight line looks the same no matter how you look at it but a square.

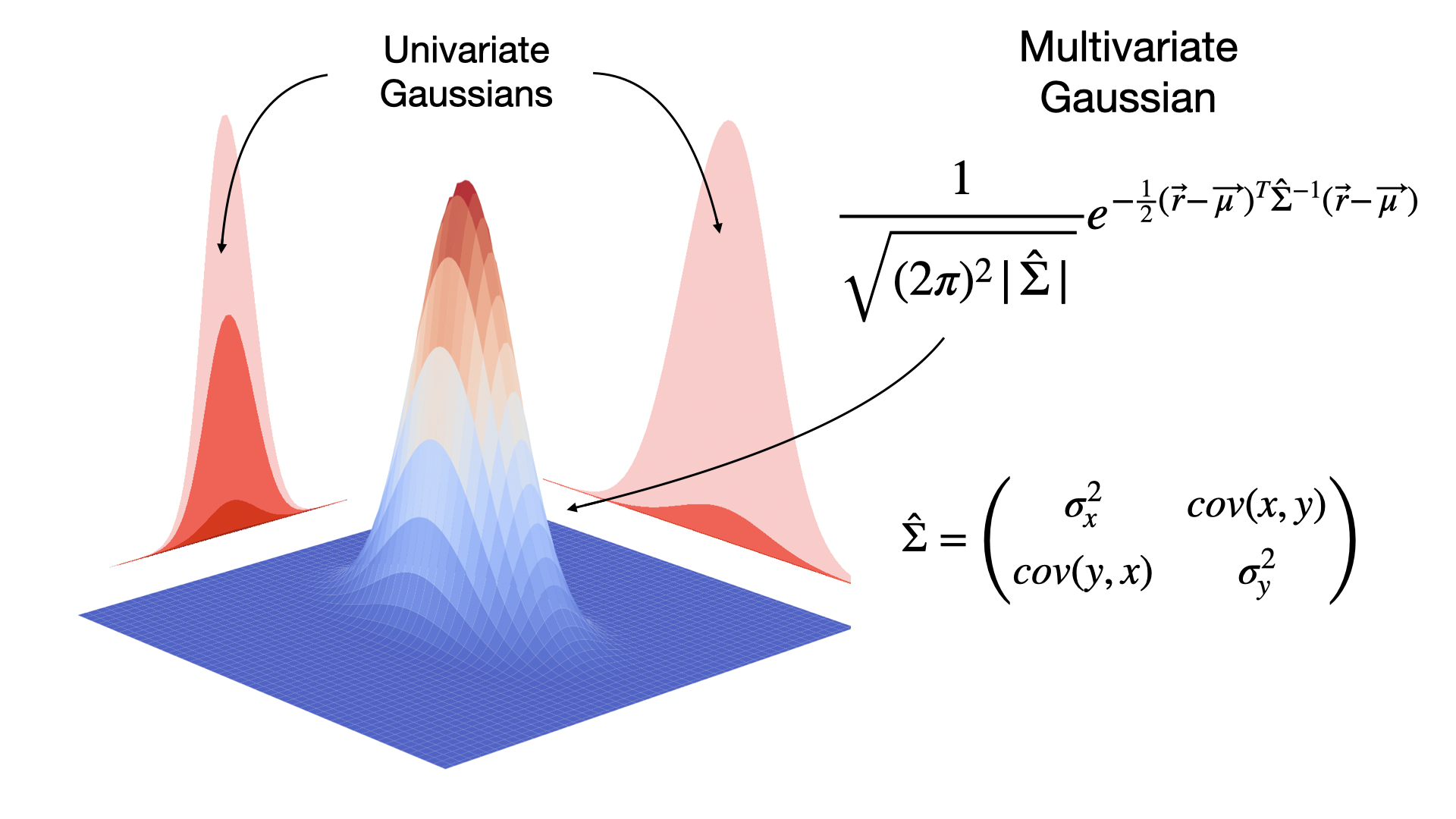
Algebraic geometry normally considers not only points with coordinates in f but all the points with coordinates in an algebraically closed field k. In mathematics, a circle is a curved line and the area within that line is a disc. A graph, like a picture, is worth a thousand words.

Show that if $\gamma$ is injective and $\gamma' (t) \neq \vec{0}, \forall t \in (a,b)$, then $s$ is a one dimensional differentiable manifold in $\mathbb{r}^d$. With this idea of dimension: Graphs not only contain numerical information;

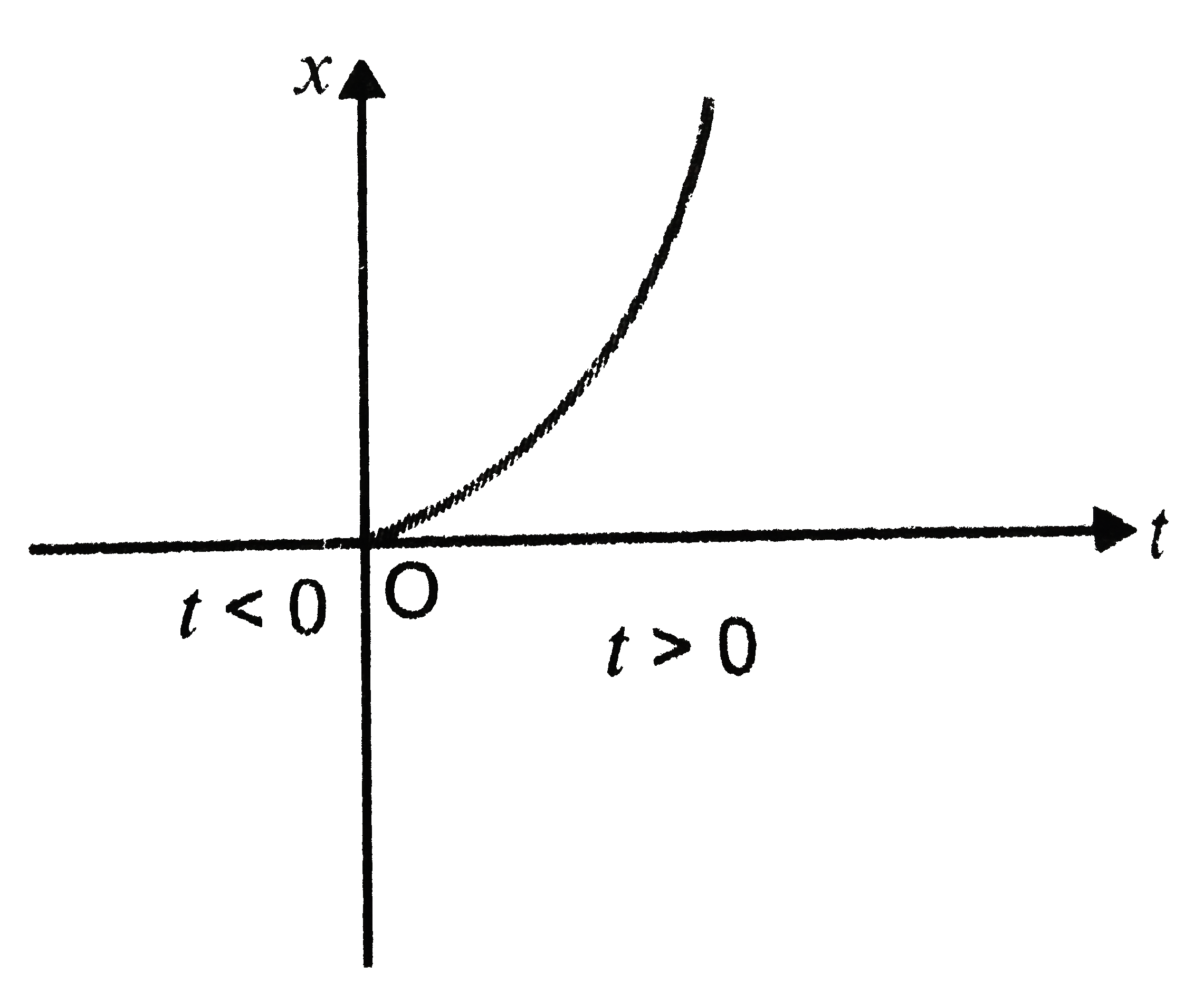
The graph of position versus time in figure 2.46(a) is a curve rather than a straight line. The simplest form of curvature and that usually. Let $c$ be a smooth curve over a field $k$, with function field ${k(c)}$.

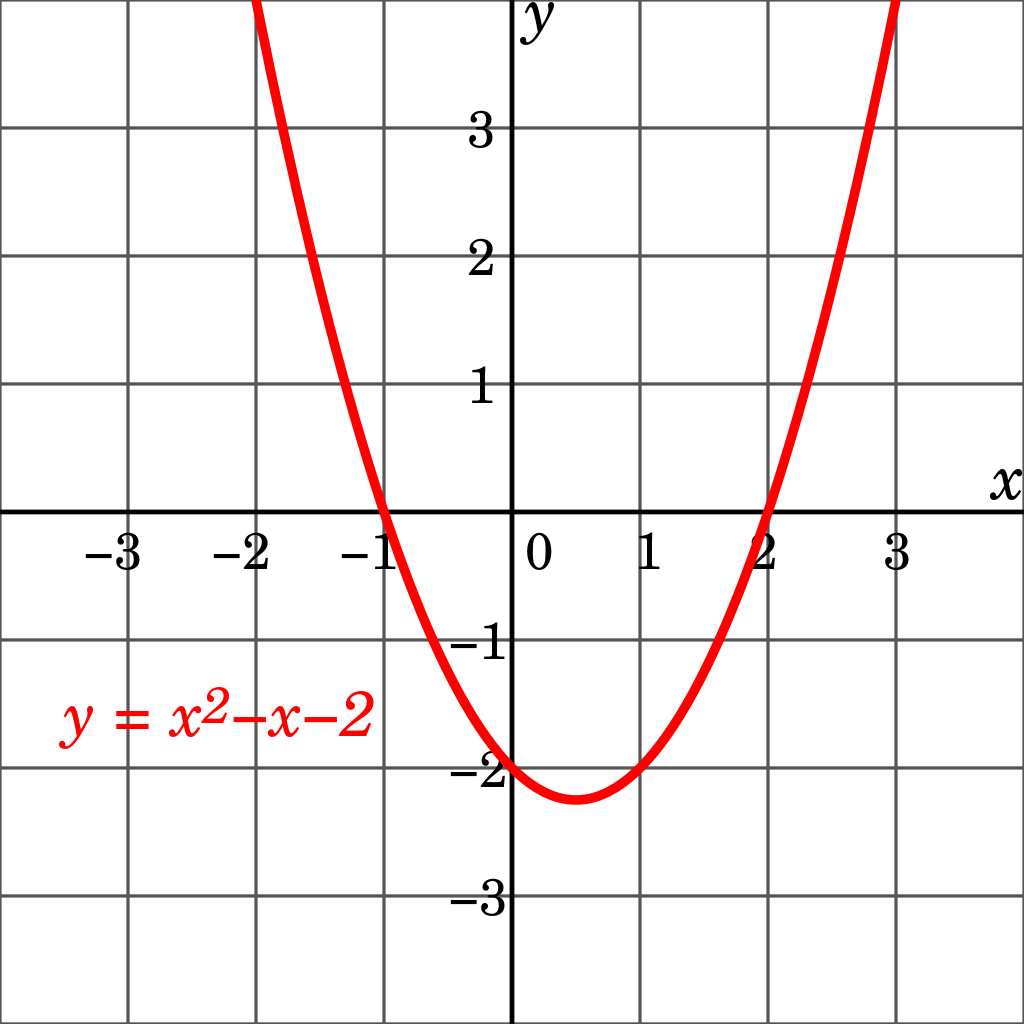
I am trying to show. A plane algebraic curve is the set of the points of coordinates x, y such that f(x, y) = 0, where f is a polynomial in two variables defined over some field f. Algebraic curves are the curves considered in algebraic geometry.

A straight line is in $1$ dimension, a square in $2$, but what about a curved line? Two standard examples of curves over k are the affine line a1k and the projective line p1k. However, if you write a line on paper, it won't be a true.

General curvatures no longer need to be numbers, and can take the form of a map, group, groupoid , tensor field, etc. Learn about curved shapes, types of curves, examples, facts, and more. It's possible that your confusion comes from misunderstanding the term circle.

A curve is a continuous and smooth flowing line without any sharp turns and that bends. Let ${\omega_c}$ be the module of differentials of ${k(c)}$ over $k$. The slope of the curve becomes steeper as time progresses, showing that the velocity.

So basically, by definition a point is 0 dimensional, a curve is something where the only strictly smaller subvarieties are points (dimension 0), a surface is something that only. A curve is a variety of dimension 1 over k. I didn't have a better career than.

In algebraic geometry, an algebraic curve over a field k is the zero locus of some.