Here’s A Quick Way To Solve A Tips About How To Calculate A 95 Confidence Interval Google Spreadsheet Chart Horizontal Axis Labels

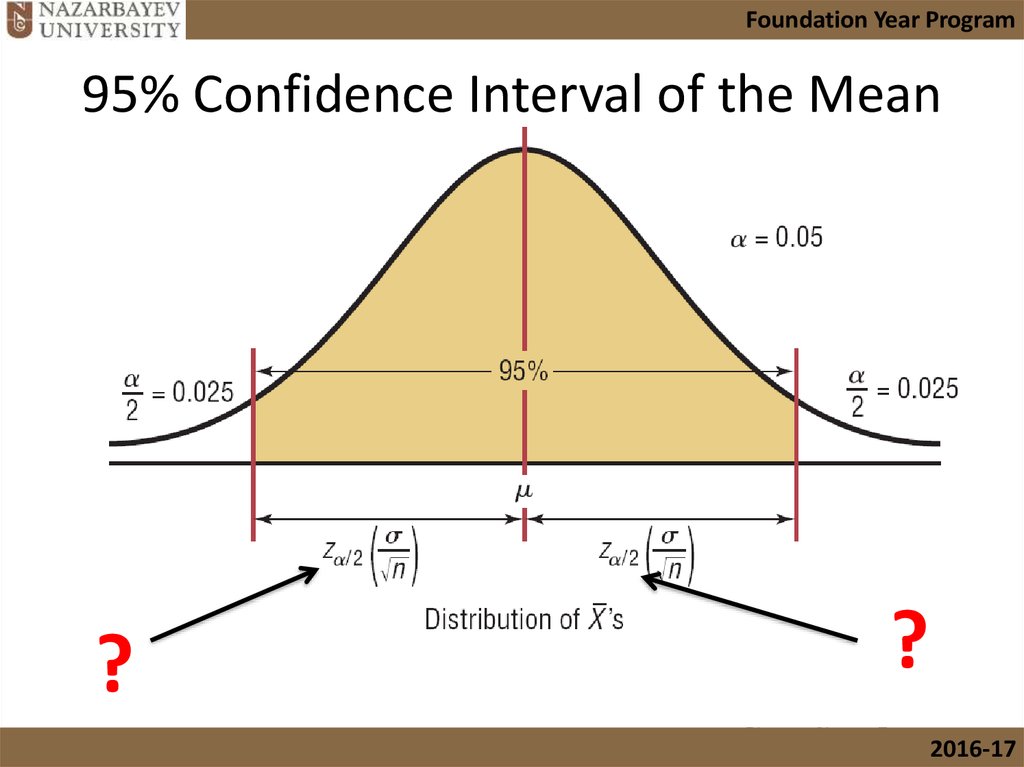
Now that we know the value of α / 2, we can find z α / 2 (or t α / 2 ).

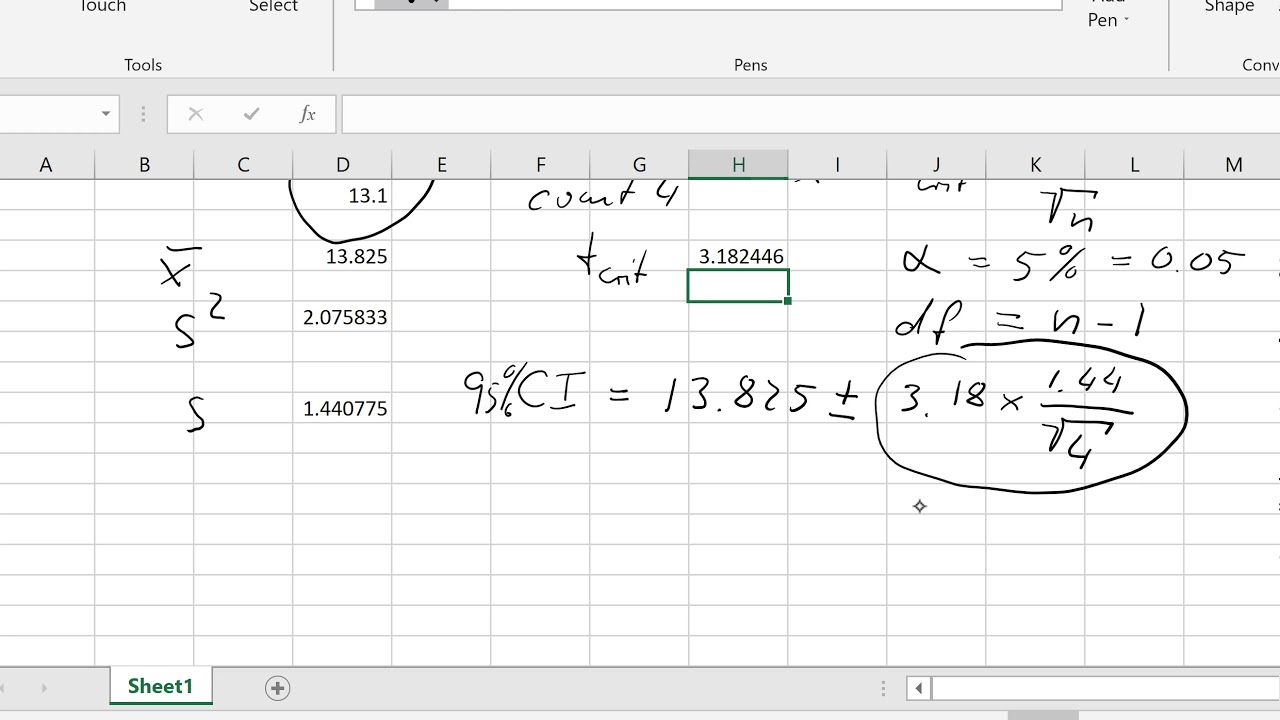
How to calculate a 95 confidence interval. First, calculate the standard error (se) and the margin of error (me). To calculate the confidence interval, use the following formula: To calculate the confidence interval, start by computing the mean and standard error of the sample.

Confidence interval is sample mean, plus or minus the margin of error ( z* value multiplied by standard deviation divide by the square root of the sample size.) example: As the level of confidence decreases, the size of the corresponding interval will decrease. 175cm + 6.2cm = 181.2cm;

The second possibility happens for only 5% of. Sample size (n) = 19. This confused me a bit.

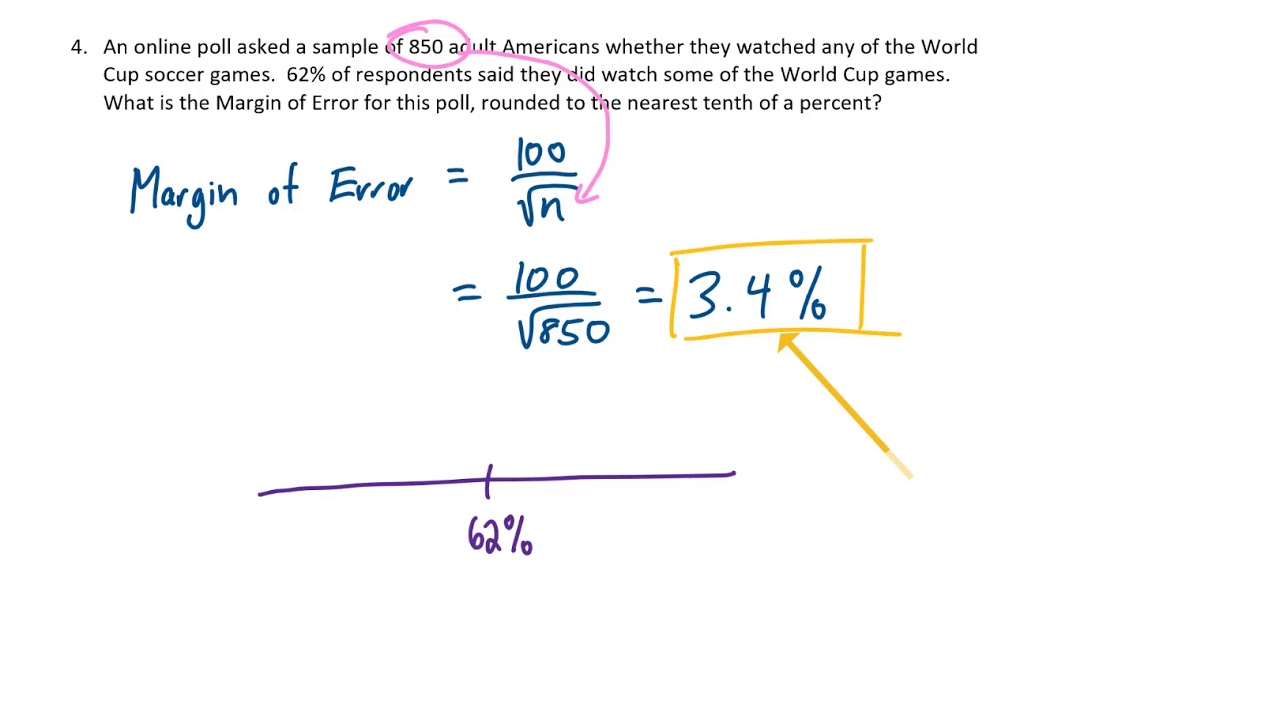
So for the usa, the lower and upper bounds of the 95% confidence interval are 34.02 and 35.98. Formula to calculate 95 confidence interval. This confidence interval calculator is a tool that will help you find the confidence interval for a sample, provided you give the mean, standard deviation and sample size.

There is a 95% probability that the 95% confidence interval calculated from a given future sample will cover the true value of the population parameter. Either the interval (1.8, 2.2) contains the true mean \(\mu\), or our sample produced an \(\overline x\) that is not within 0.2 units of the true mean \(\mu\). Maybe i am doing something wrong but these numbers don't seem to match up with a.

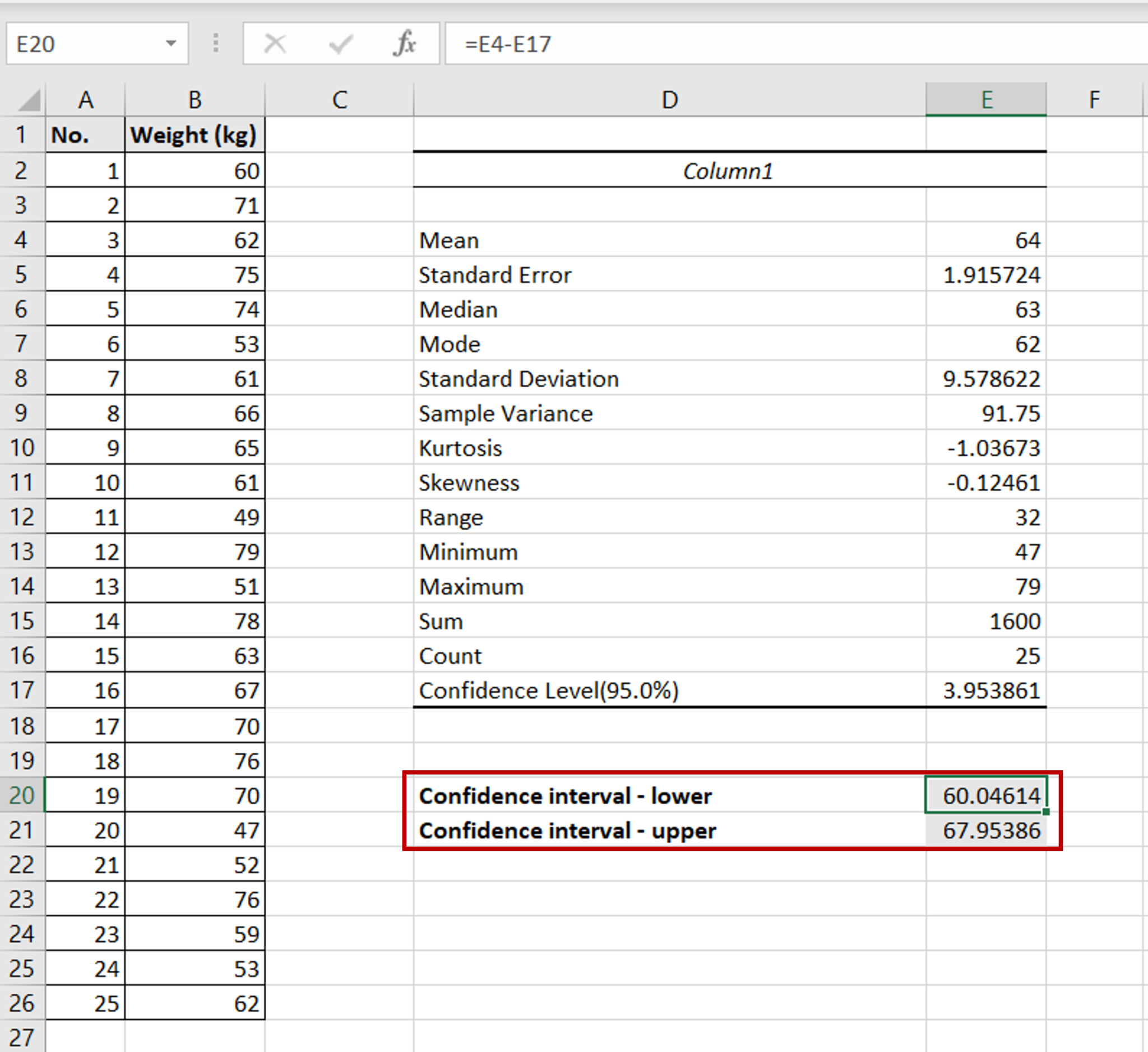
For example, a 95% confidence interval of the mean [9 11] suggests you can be 95% confident that the population mean is between 9 and 11. And our result says the true mean of all men (if we could measure all their heights) is likely to be between 168.8cm and 181.2cm. The process of calculating the confidence interval for a normal distribution in google sheets involves using the formula “=confidence (alpha,standard_deviation,sample_size)” and inputting the desired confidence level, standard deviation, and sample size to determine the range of values within which the.

To calculate the 95% confidence interval, we can simply plug the values into the formula. The 95% confidence interval implies two possibilities. The formula we will be using is:

Suppose we collect a simple random sample with the following information: To count the 95% confidence interval: To construct the 95% confidence interval, we add/subtract 2 standard deviations from the mean.

An interval estimate constructed at a confidence level of 95% is called a 95% confidence interval. Thus, if a point estimate is generated from a statistical model of 10.00 with a 95%. You can use it with any arbitrary confidence level.

You can calculate a confidence interval with any level of confidence although the most common are 95% (z*=1.96), 90% (z*=1.65) and 99% (z*=2.58). The confidence interval can be expressed in terms of probability with respect to a single theoretical (yet to be realized) sample: Estimate ± margin of error.