Exemplary Tips About How To Tell If A Line Of Best Fit Is Good Based On Residuals Plot Two Time Series With Different Dates

{ (1, 3) (2, 4) (3, 3) (4, 7) (5, 6) (6, 6) (7, 7) (8, 9)}.
How to tell if a line of best fit is good based on residuals. Figure 1 is an example of how to visualize residuals against the line of best fit. Also known line of best fit or a trend line. First, let's look at the residuals of a line that is a good fit for a data set.
We can use the line to make predictions. Anomalies are values that are too good, or bad, to be true or that represent rare cases. First recall that the linear best fit line is the line which minimizes the sum of squared residuals (see least squares):
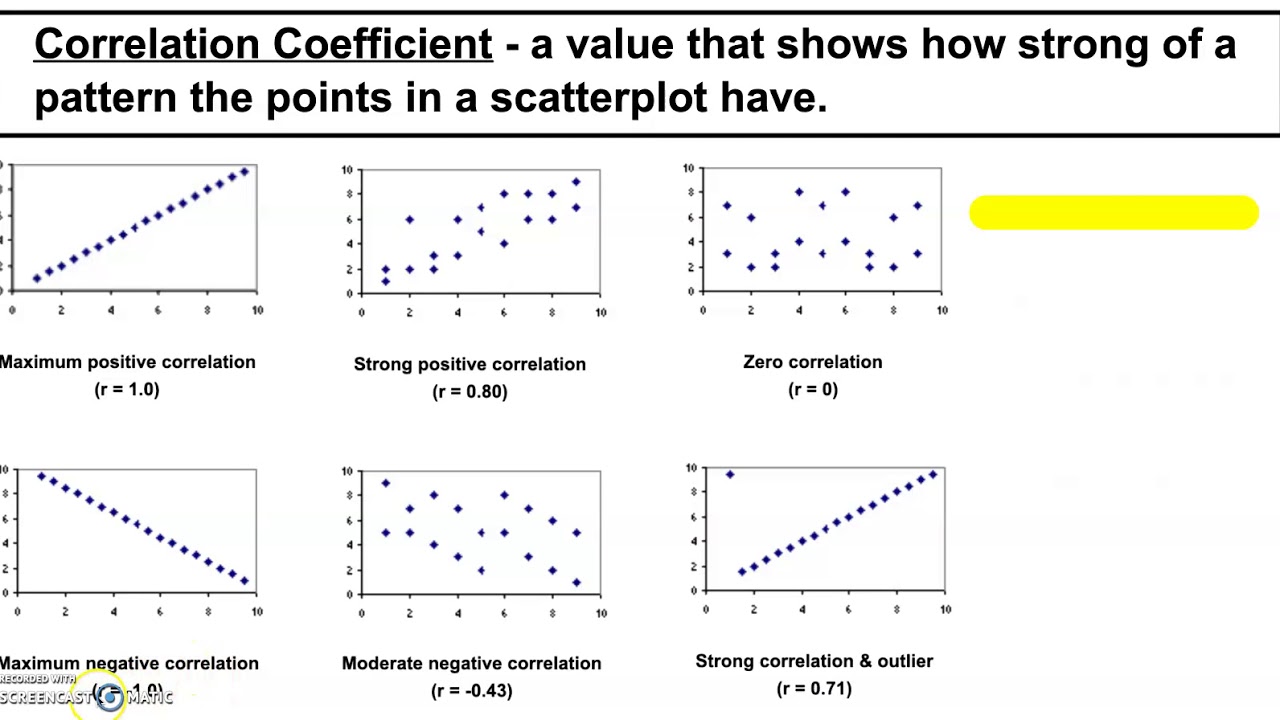
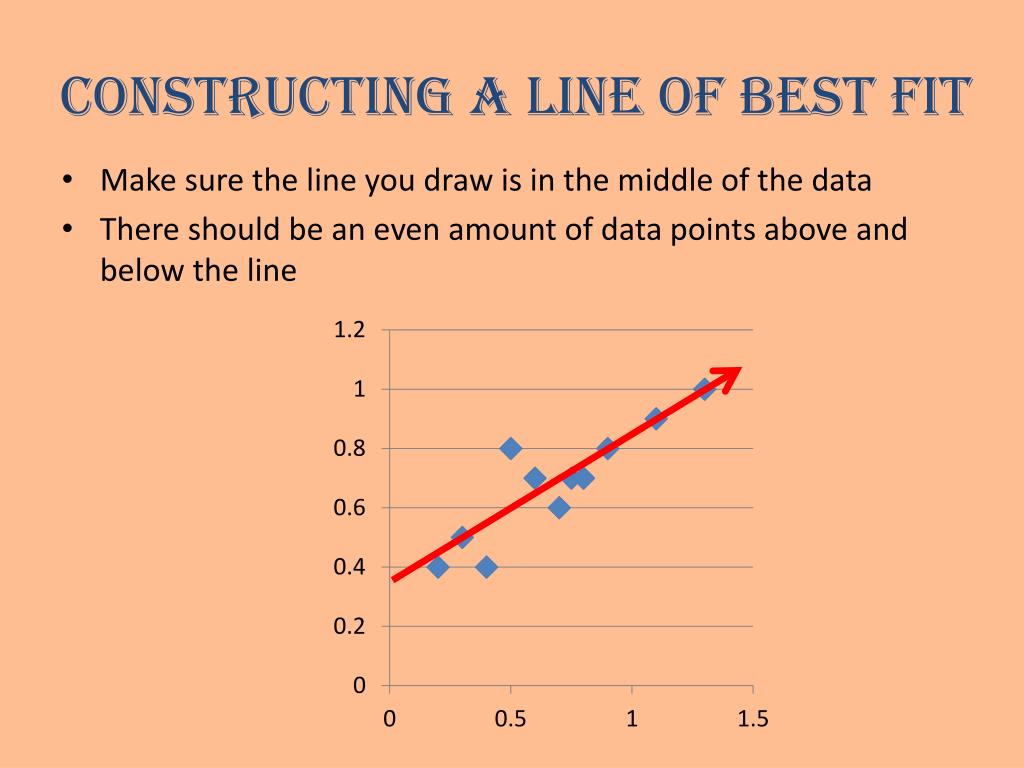
For data points above the line, the residual is positive, and for data points below the line, the residual is negative. Residuals are the leftover variation in the data after accounting for the model fit: The term “best fit” means that the line is as close to all points (with each point representing both variables for a single person) in the scatterplot as possible, with a balance of scores above and below the line.
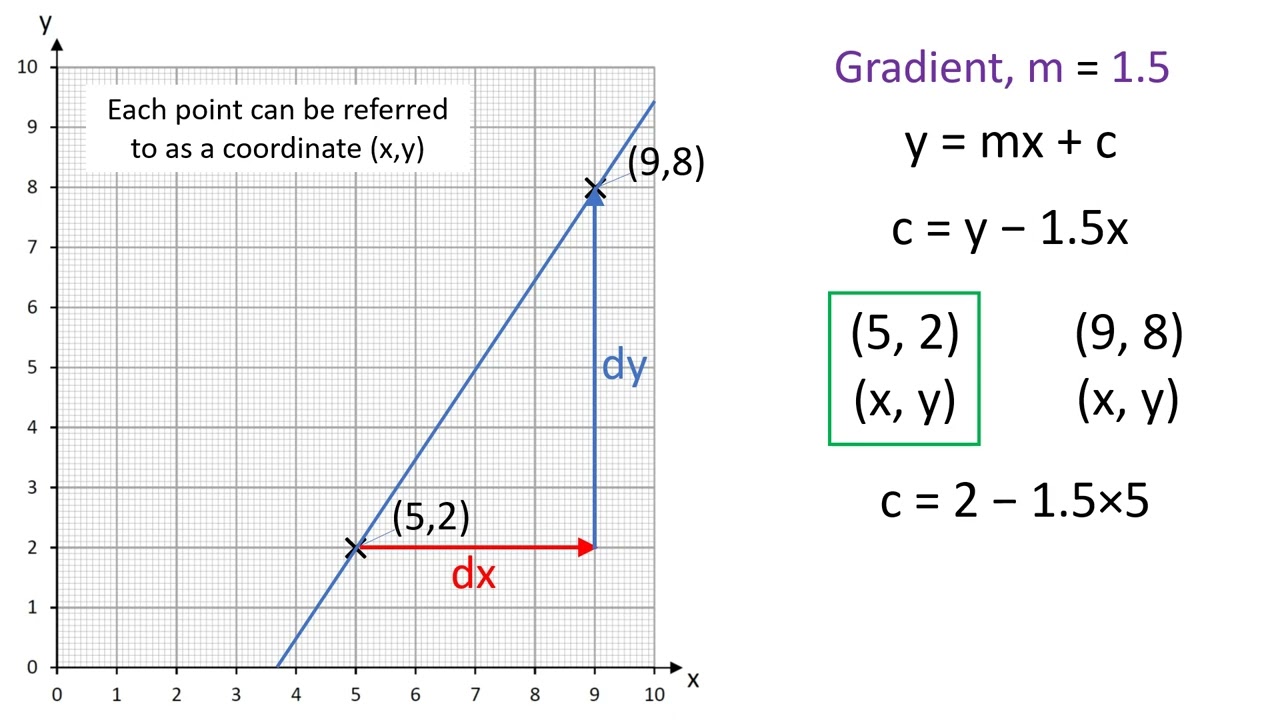
A least squares regression line represents the relationship between variables in a scatterplot. In a “bad” residual plot, the residuals exhibit some type of pattern such as a curve or a wave. The formula for this line of best fit is written as:
Highlights by topic. The p value is the probability of finding the observed results when. A value closer to 1 (100%) is usually good.
$$\sum_{i=1}^{n}{r_i^2}$$ where $r_i$ is the residual for data point $i$, and $n$ is the number of data points. The line of best fit is used to express a relationship in a scatter plot of different data. It is a scatter plot of residuals on the y axis and fitted values (estimated responses) on the x axis.
Y = c + b1(x1) + b2(x2) where, y is dependent variable. When conducting a residual analysis, a residuals versus fits plot is the most frequently created plot. The vertical lines are the residuals.
The linear regression model attempts to find the relationship between variables by finding the best fit line. Chris and stevie discuss the latest rangers news in monday's morning briefing. Observations below the line have negative.
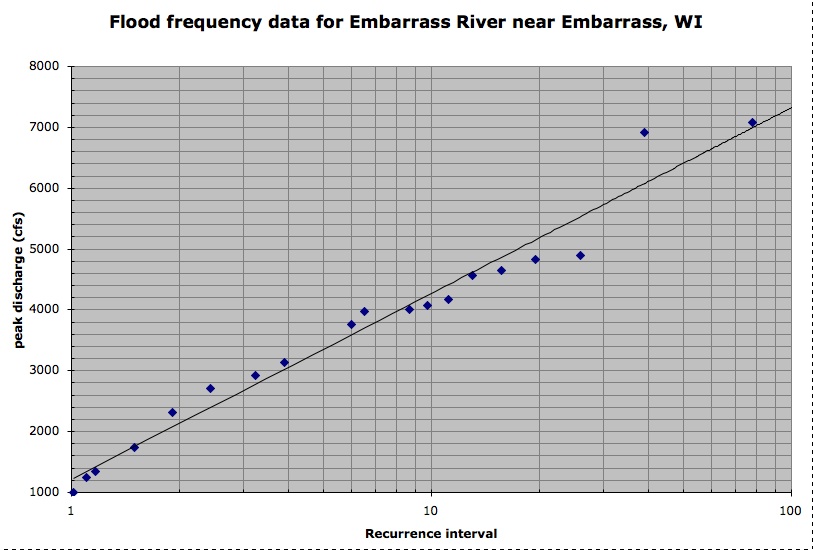
A line was fit to the data to model the relationship. This is an indication that the regression model we used is. Generative ai can revolutionize tax administration and drive toward a more personalized and ethical future.
Estimating with linear regression (linear models) a line of best fit is a straight line that shows the relationship between two sets of data. A line of best fit is used to show a trend between points. \[\text {data} = \text {fit + residual}\] each observation will have a residual.


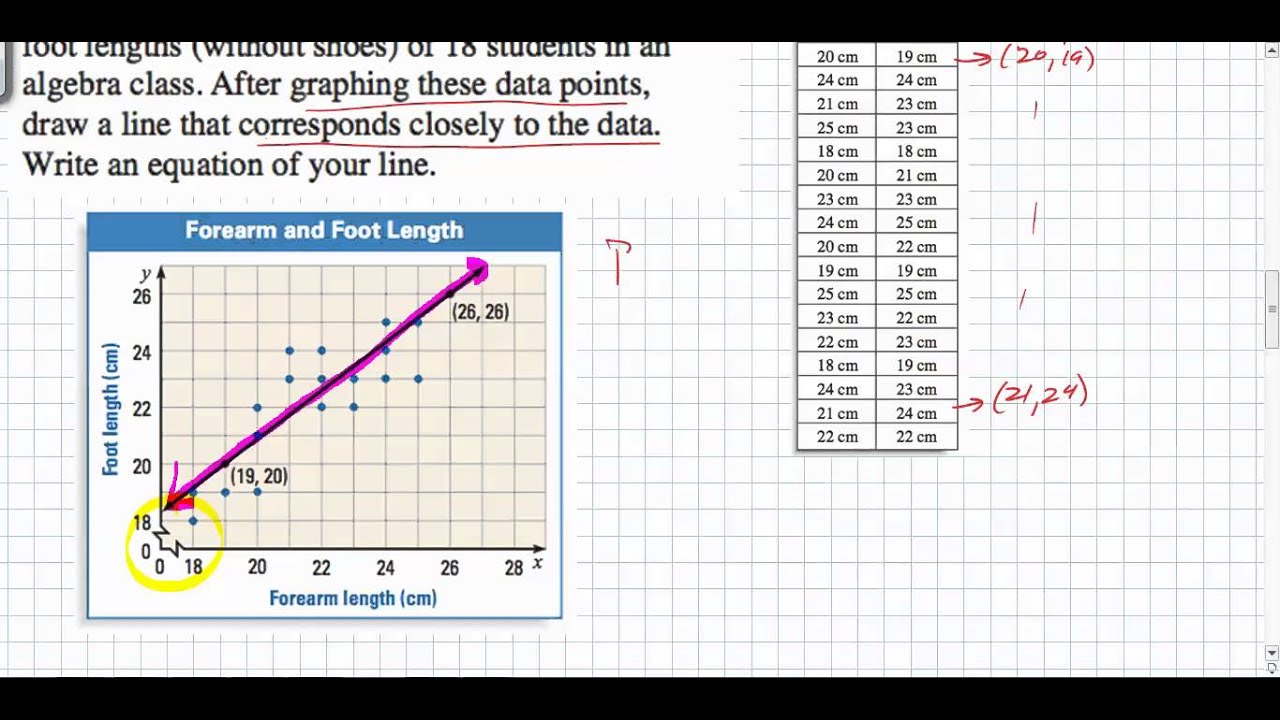

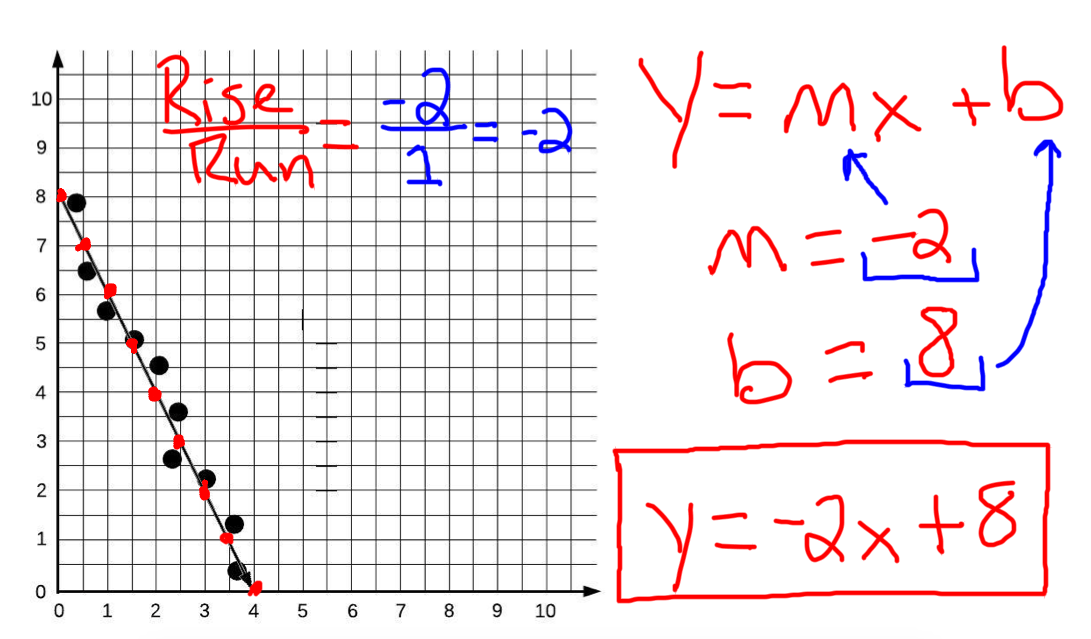
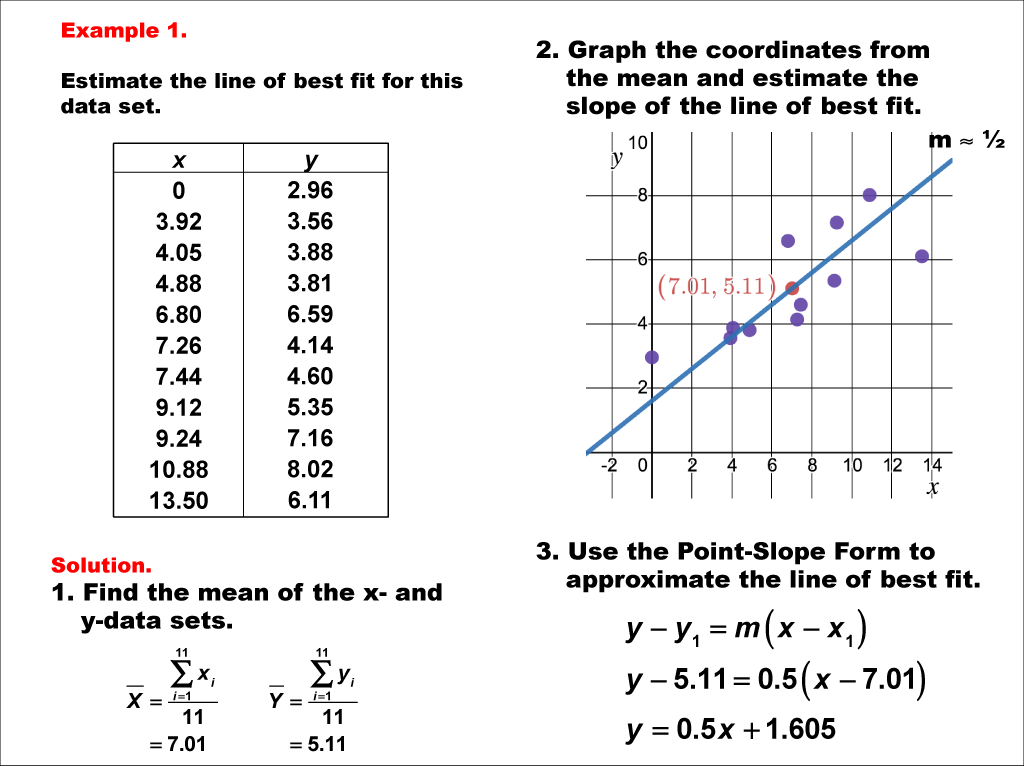
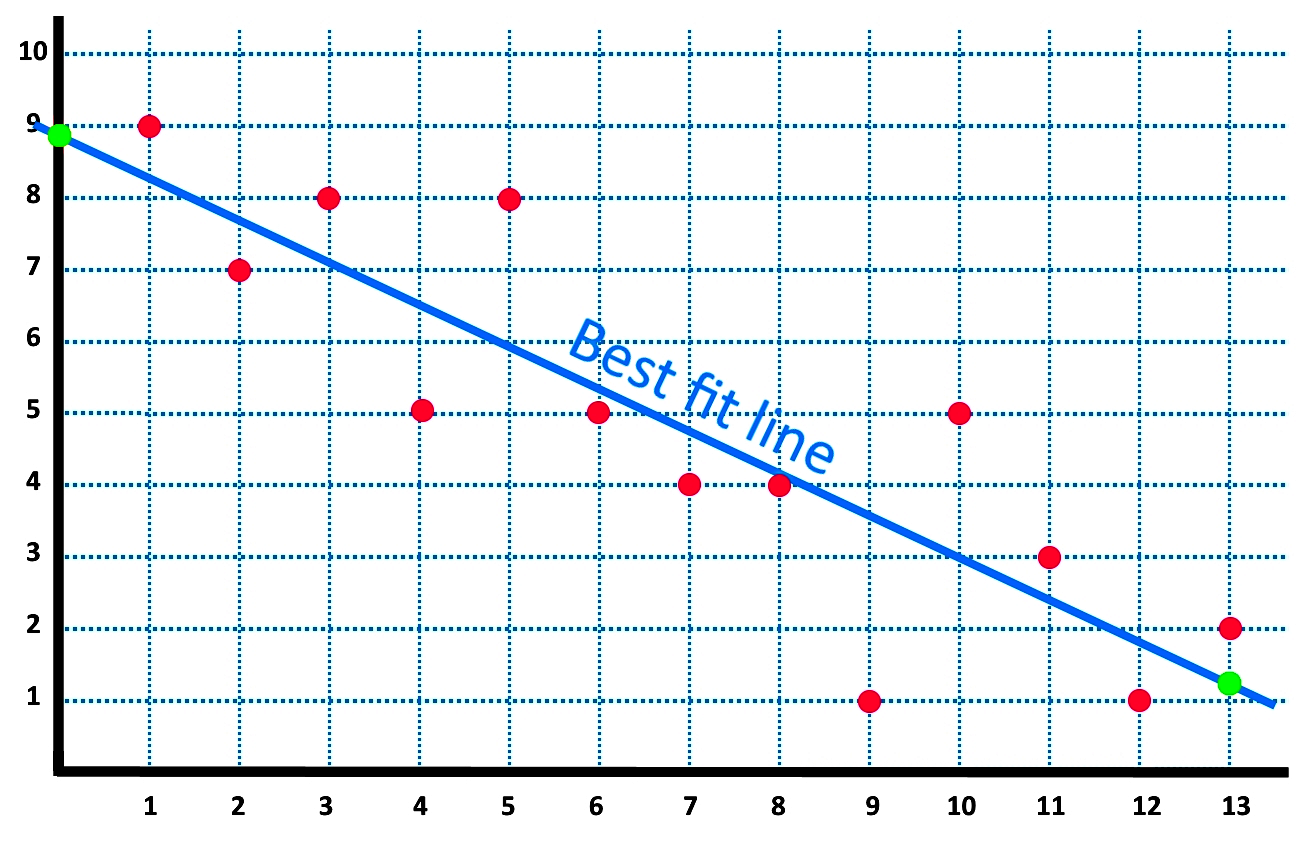










:max_bytes(150000):strip_icc()/Linalg_line_of_best_fit_running-15836f5df0894bdb987794cea87ee5f7.png)
