Outrageous Info About Is A Parabola Smooth Curve How To Draw Graph

However, in this parameterization, the curve is not smooth.

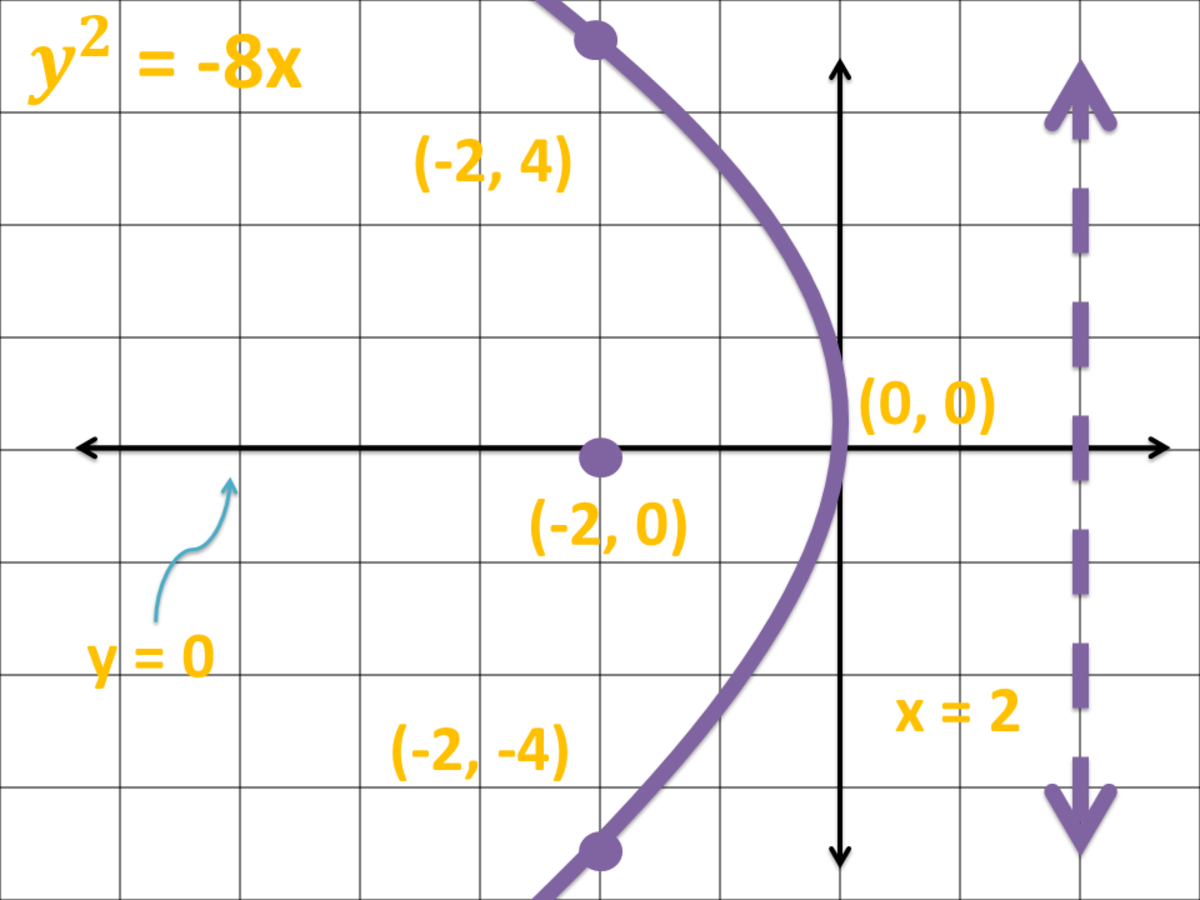
Is a parabola a smooth curve. Of the parabola can help us to find an easier parameterization of the holditch curve that will also. It satisfies the condition of non smooth curve i.e. Parabolas are also symmetrical which means they can be folded along a line so that all of the points on one side of the fold line coincide with the corresponding points on the other side of the fold line.

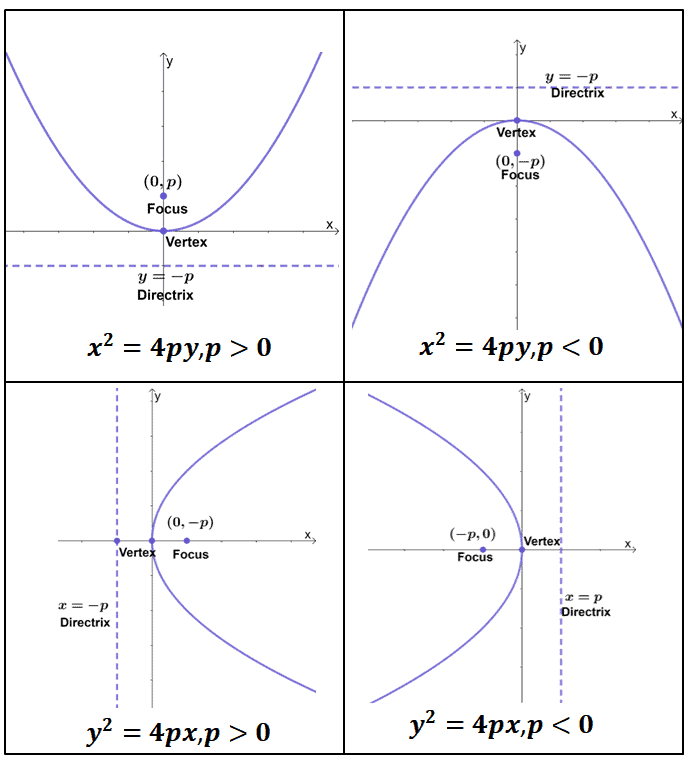
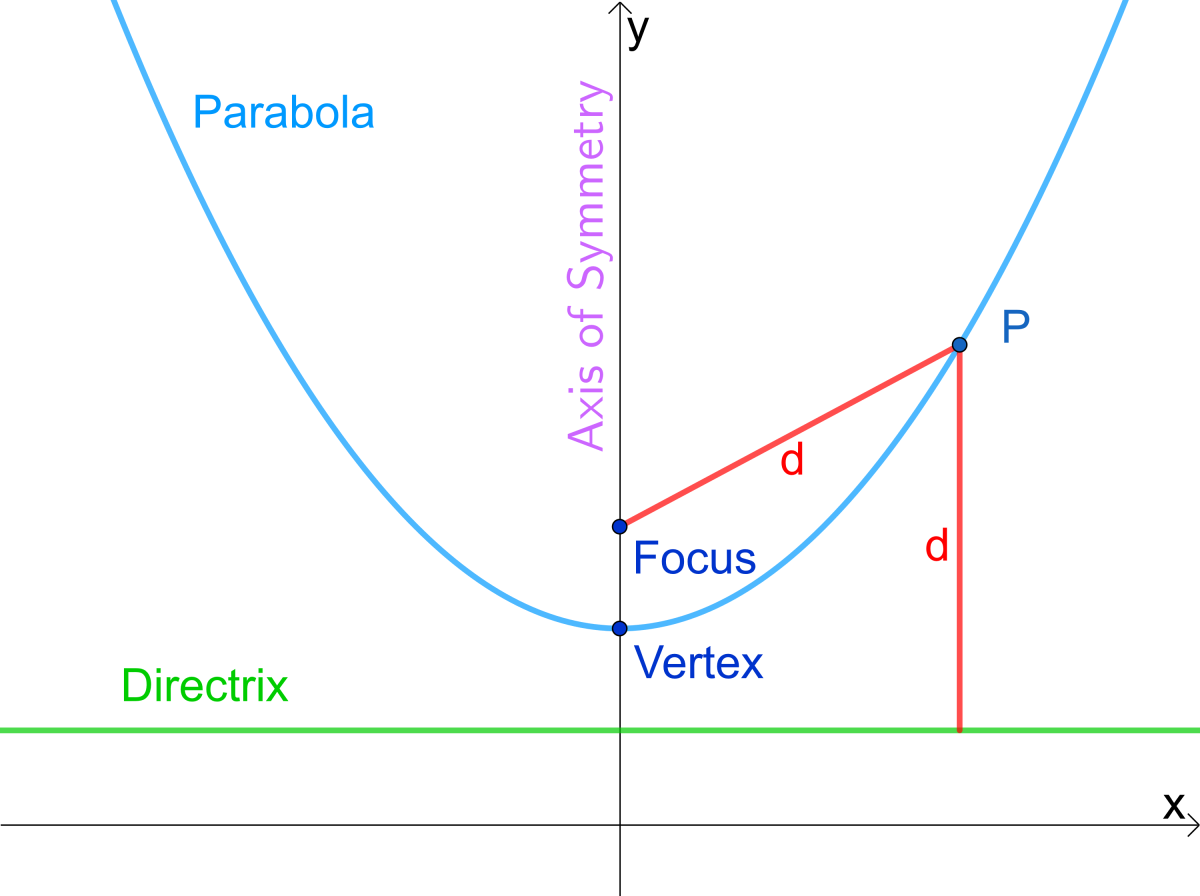
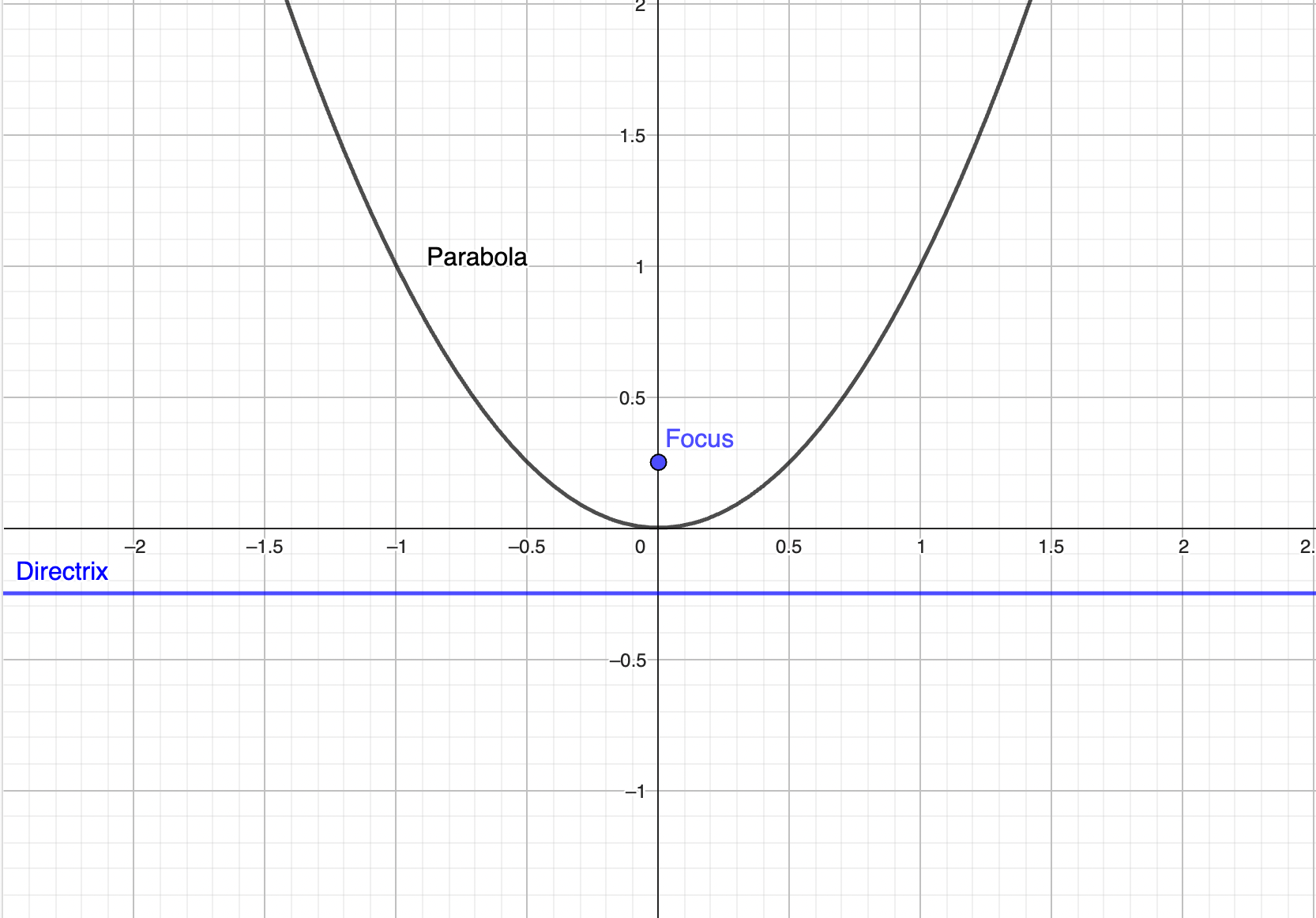
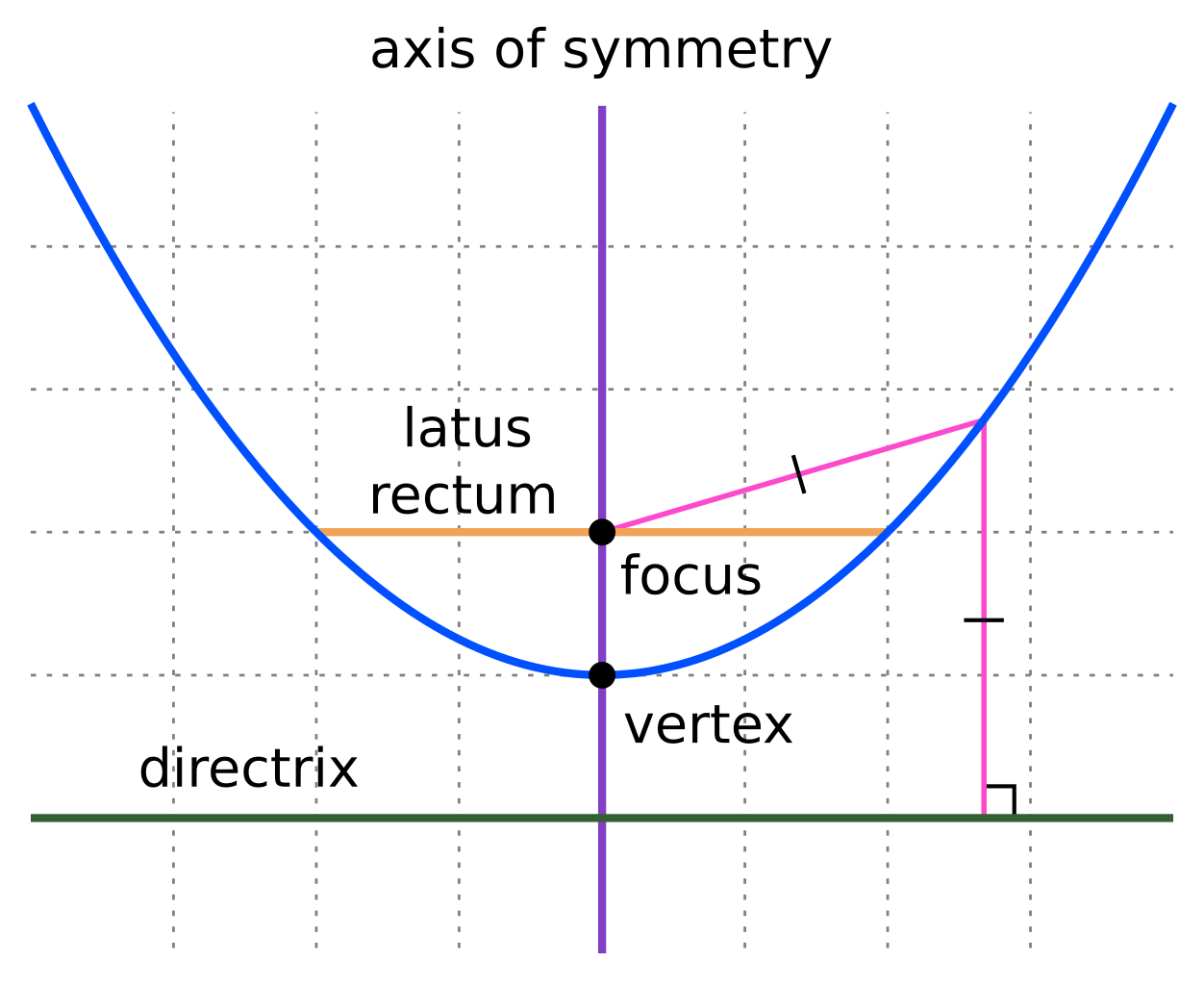
The parabola is a smooth curve without any sharp points. The first derivative, second derivative, third and so on are all continuous, so you get a smooth curve. The fixed point is called the focus of the parabola, and the fixed line is called the directrix of the parabola.

The parabola is the curve formed from all the points (x, y) that are equidistant from the directrix and the focus. As a plane curve, it may be defined as the path (locus) of a point moving so that its distance from a fixed line (the directrix) is equal to its distance from a fixed point (the focus). Holditch curves have already been studied from the parametric point of view, although numerical methods and approximations are often necessary for their computation.

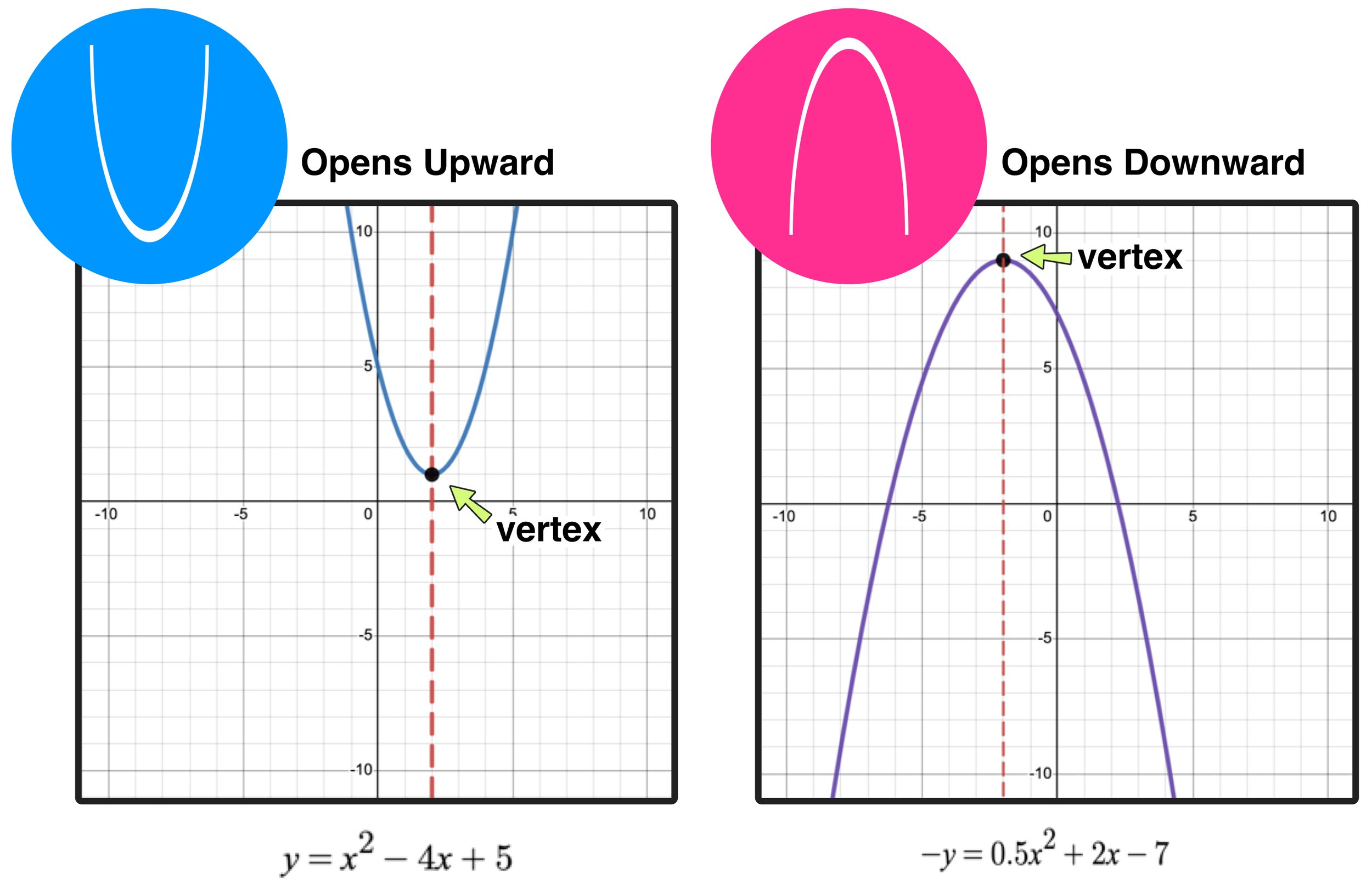
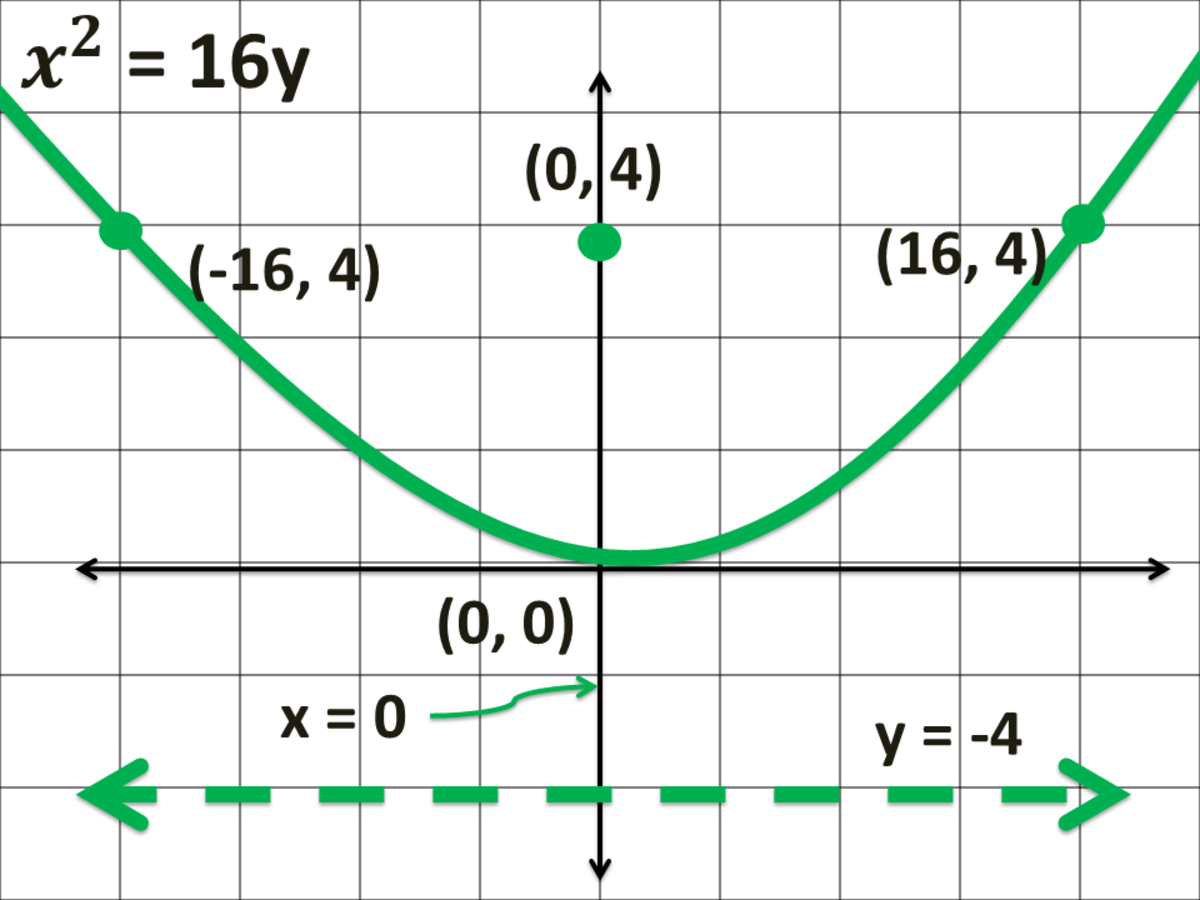
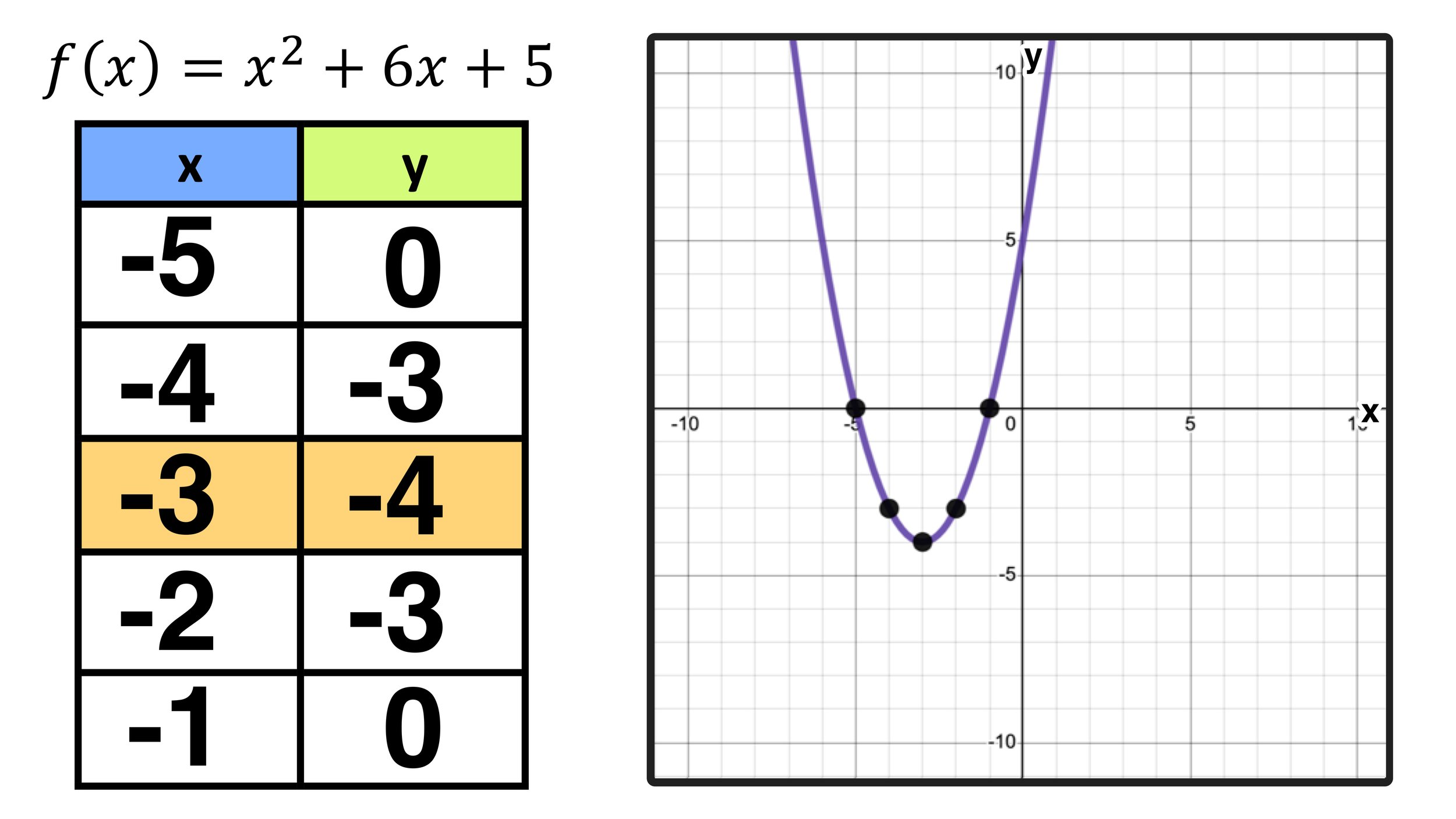
For instance, one can verify that x = t 3, y = t 6 produce the familiar y = x 2 parabola. Below are two parabola graph examples, one in which the parabola opens upwards and one in which it opens downwards: When we plot these points and join them with a smooth curve, we obtain the quadratic graph shown above.

The curve is called a parabola. A parabola, a convex curve that is the graph of the convex function. For example, the following parametrization:

The line perpendicular to the directrix and passing through the focus (that is, the line that splits the parabola up the middle) is called the axis of symmetry. If $r(t)=t^2 i + t^4 j$, then it is a parabola $y = x^2$. Graphs of y = ax ², a > 0.

The curve is called a parabola. A curve \(c\) defined by \(x=f(t)\), \(y=g(t)\) is smooth on an interval \(i\) if \(f^\prime\) and \(g^{\prime}\) are continuous on \(i\) and not simultaneously 0 (except possibly at the endpoints of \(i\)). A smooth motion of such a chord with its endpoints always lying on \.

For example, when you shoot a basketball, the path of the ball creates a parabola. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves. The lower, the better the fit will approach the original data, the higher, the smoother the resulting curve will be.

A fixed point (the focus ), and. But geometrically it shows the curve (parabola) is smooth at $(0,0)$. A particle traveling along the parabola according to the given parametric equations comes to rest at t = 0, though no sharp point is created.

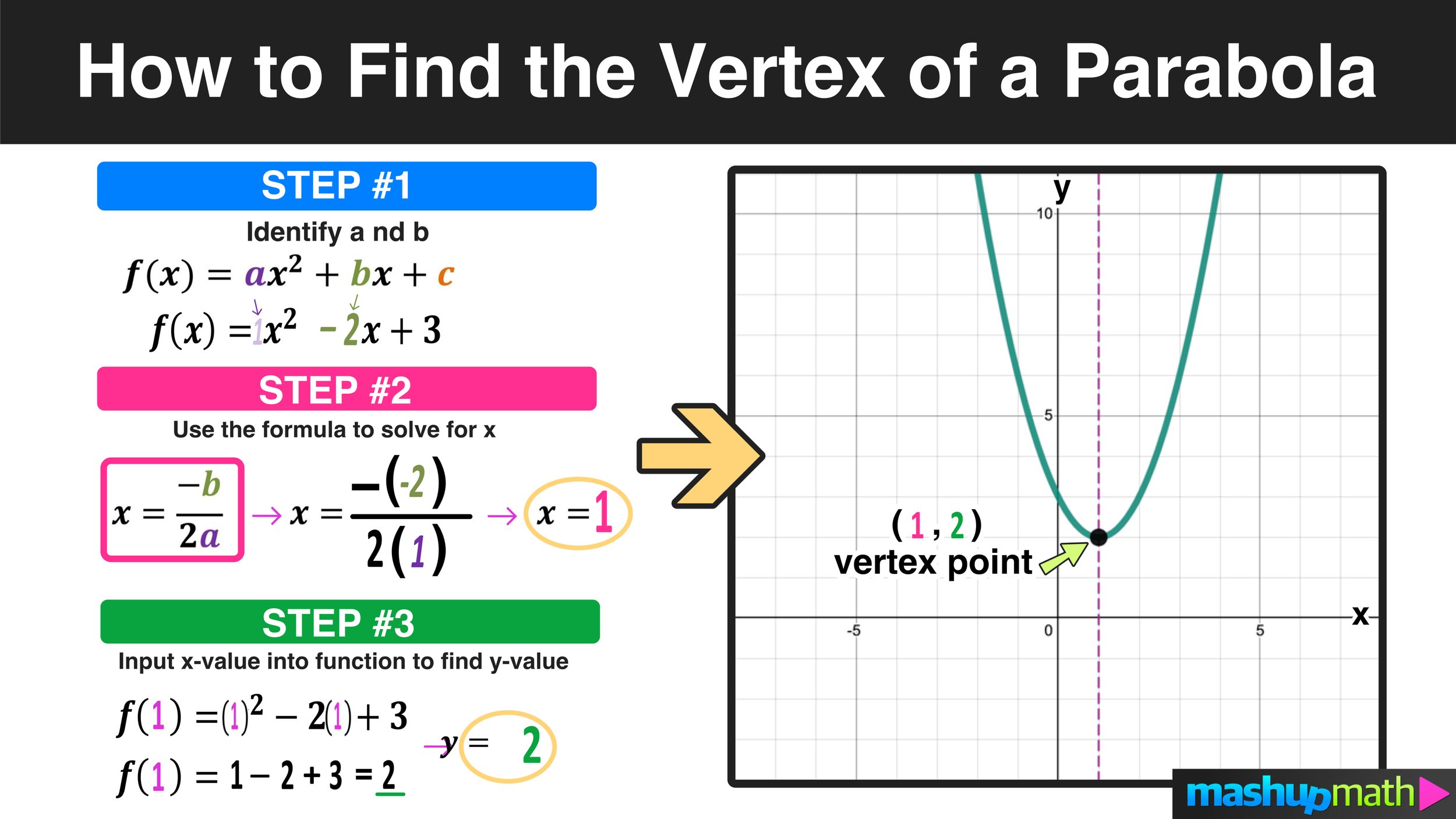
X(t) = t, y(t) = t2. Parabolas exist in everyday situations, such as the path of an object in the air, headlight shapes. As we can see the minimum value of this parabola is at zero, zero.