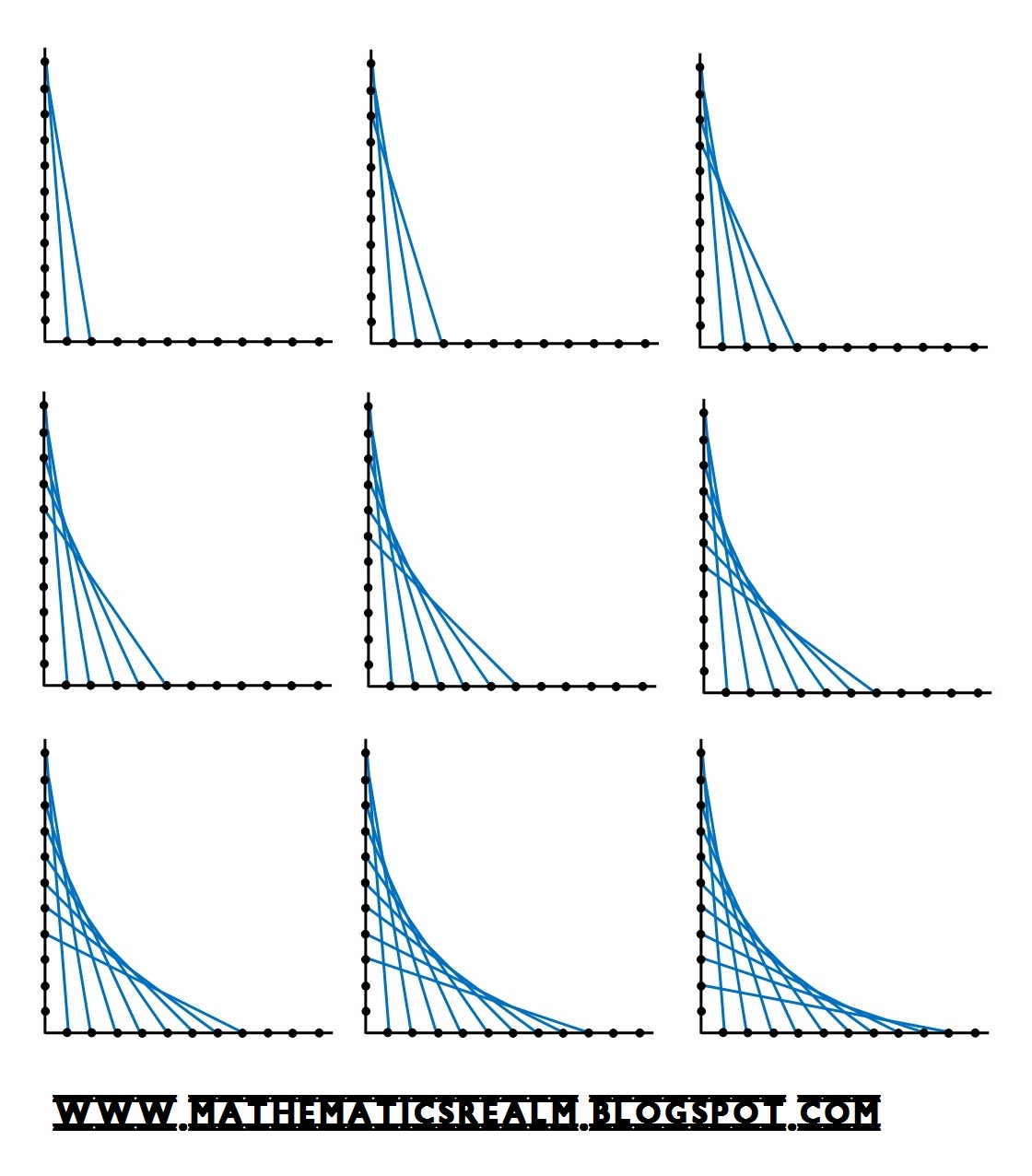
Marvelous Info About What Is A Curve In Maths Line Of Best Fit Python

We study integral plane curves meeting at a single unibranch point and show that such curves must satisfy two equivalent conditions.

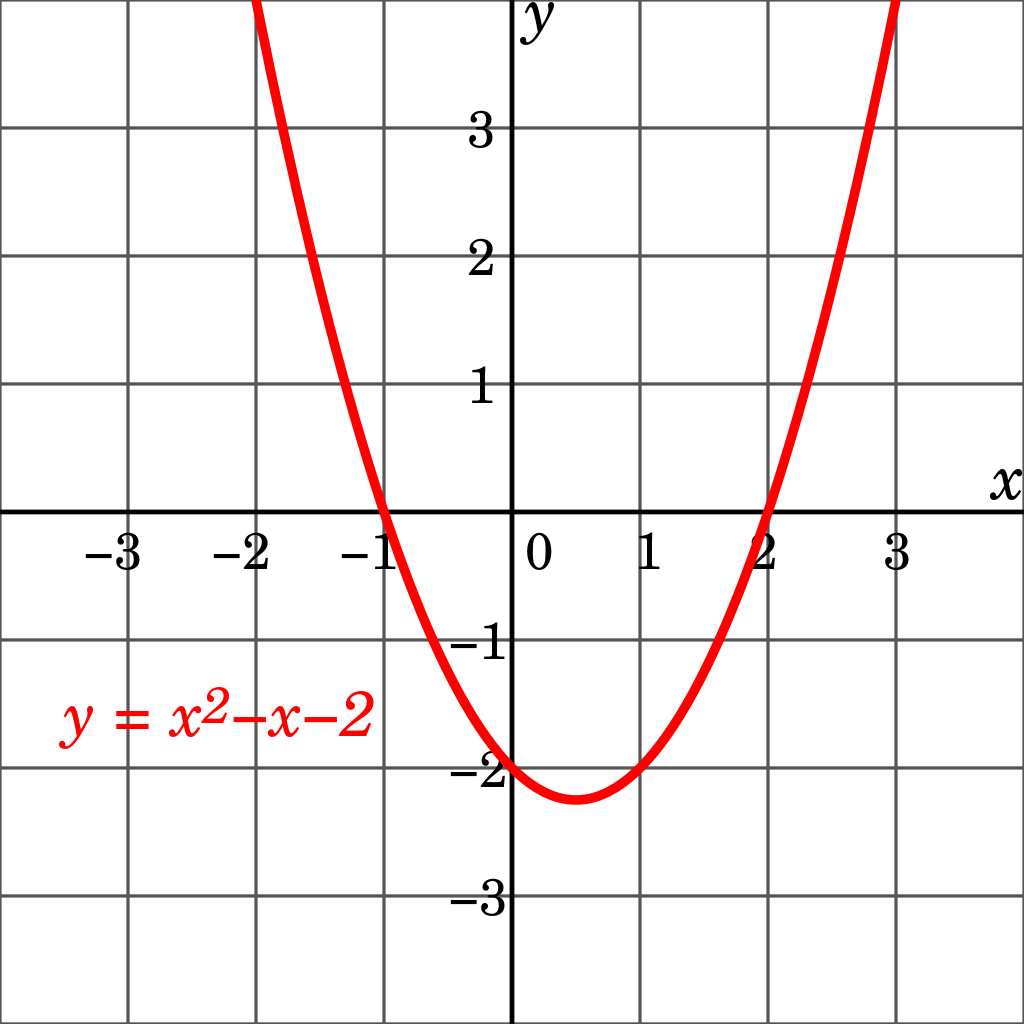
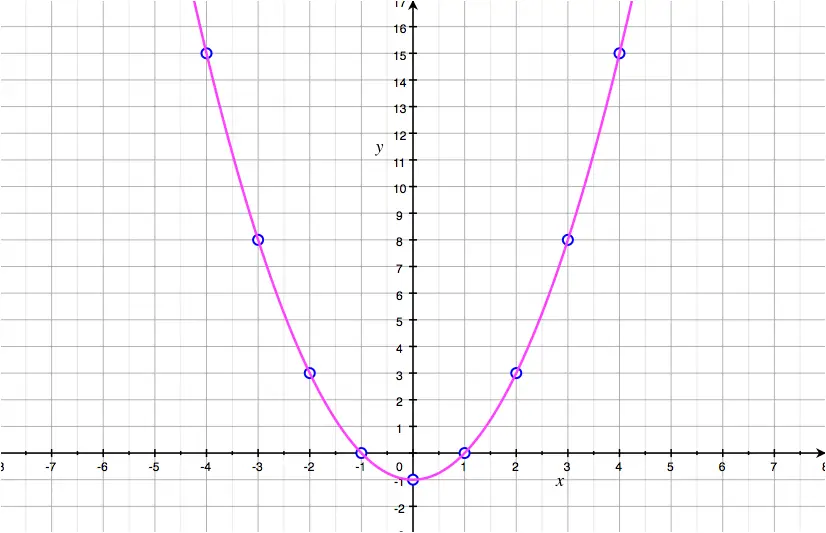
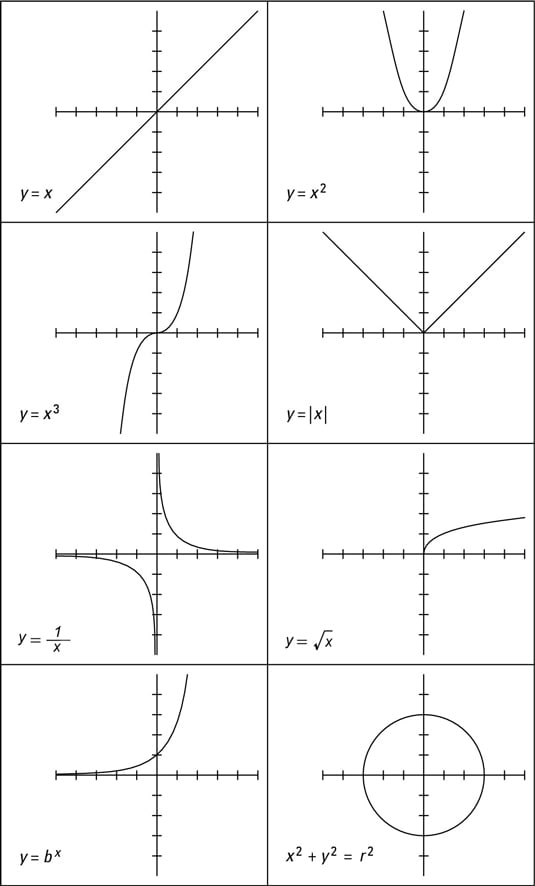
What is a curve in maths. The word can also apply to a straight line or to a series of line segments linked end to end. All quadratic graphs will be curved. Intuitively, a curve may be thought of as the trace left by a moving point.

Without further assumptions, a curve is any continuous map from i i into a topological space, or sometimes from r r into a topological space. The pictures that are the results of doodling are called curves. When is a 'curved surface' flat?

A curve is a continuous and smooth flowing line without any sharp turns and that bends. We shall only briefly mention curves in the plane and then move on to discuss positive and negative curvature of surfaces. The cardinal principle of analytic geometry is that an equation f(x, y) = 0 describes a curve which is the locus of all and only those points p(x, y) whose coordinates satisfy the given equation.

Oct 30, 2016 at 10:51. A curve is a path that deviates from a straight line gradually. A closed curve is a path that repeats.

In other words, curved lines are a form of a line that has some bent in it. How curved is a surface? In today's mathematical usage, for a precise distinction, a curve is something that is bent, whereas a line is something that is straight.

In mathematics, a curve can be straight. When we look really closely at any part of a curve it looks like a line: Such a path is usually generated by an equation.

The tropical curves that we associate to the contact point must be isomorphic. The way to identify the curve is that the line bends and changes its direction at least once. Mathematics (including geometry, statistics, and applied mathematics), physics, engineering, economics, medicine, biology, psychology, ecology, etc.

The local invariants of the curves at the contact point must be arithmetically related. A curve can be identified easily by observing if it bends and modifies its course at least once. Note also that two different paths may have the same image.

You are cordially invited to the seminar organized by the department of mathematics. Before you learnt differentiation, you would have found the gradient of a curve by drawing a tangent and measuring the gradient of this. How does the curvature change as you go around the ellipse?

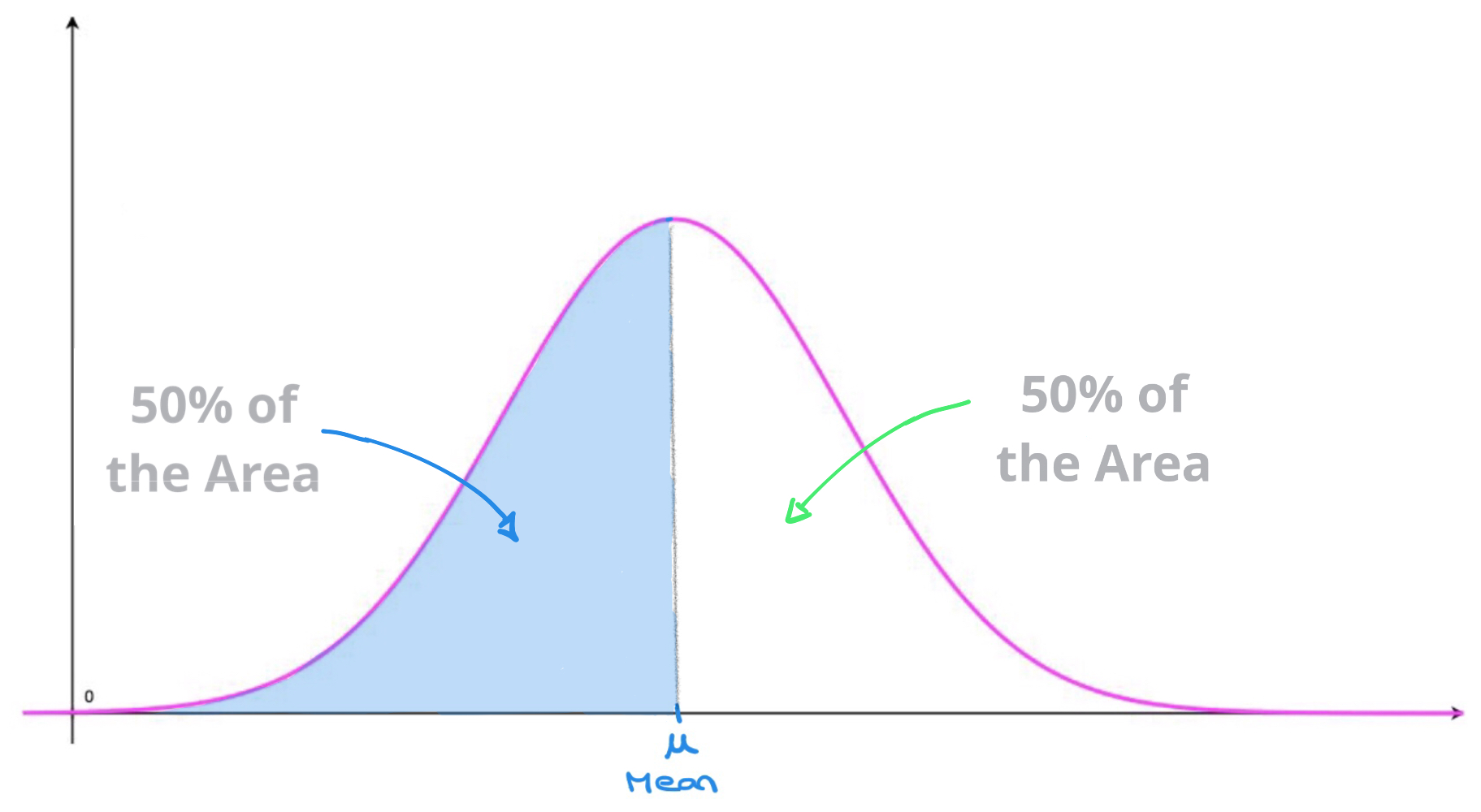
The quantity f ( v) ‍ gives the probability density as a function of the speed v ‍. Sometimes there are further assumptions, such as a differentiable curve, piecewise differentiable, piecewise linear, etc. As drawn in the picture, you get a parametric curve with: