Fun Tips About How To Determine If A Graph Is Smooth Plot Linestyle Python

Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more.

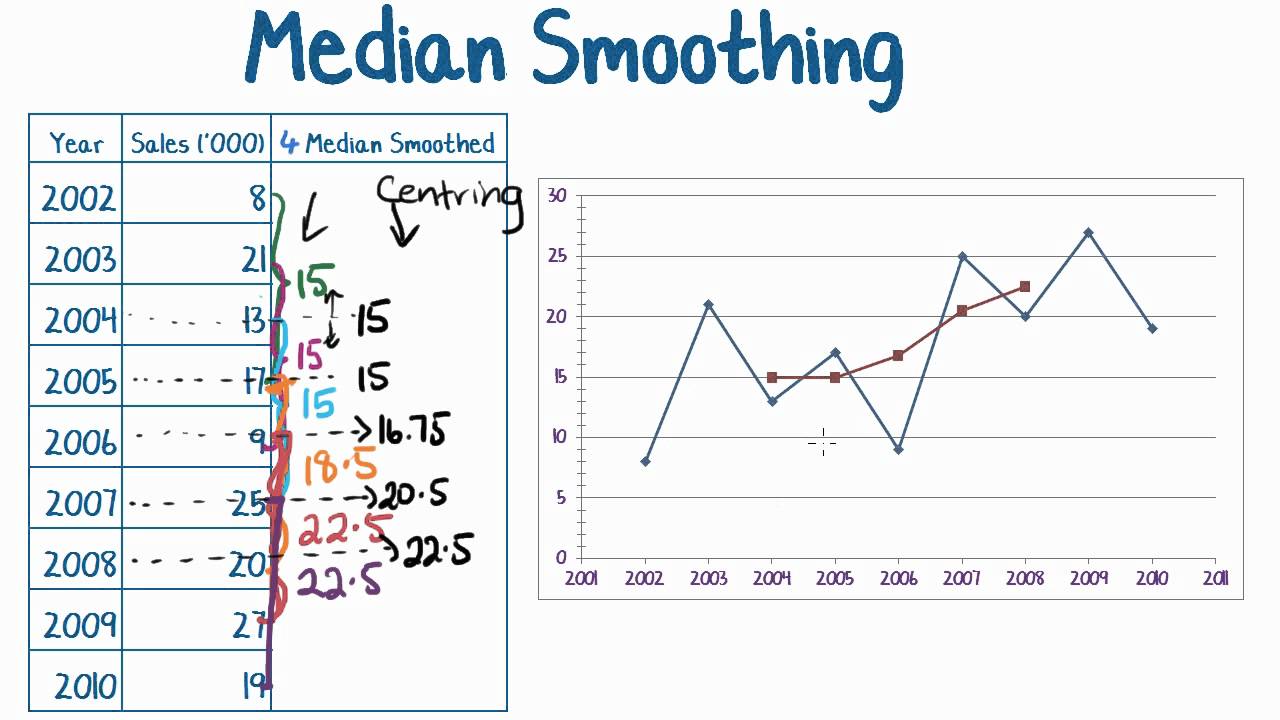
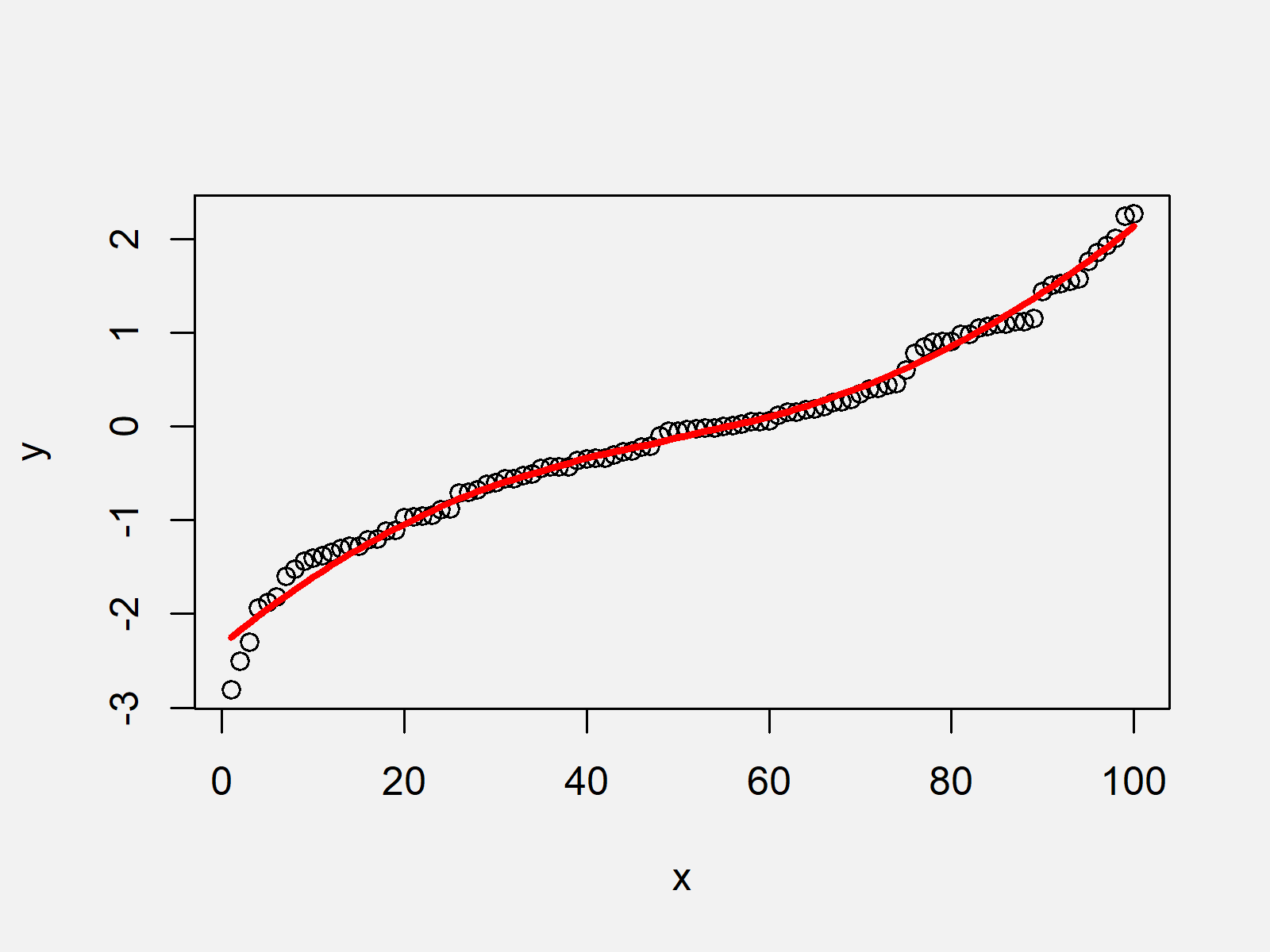
How to determine if a graph is smooth. Explore math with our beautiful, free online graphing calculator. Given a graph, use the vertical line test to determine if the graph represents a function. Larger values will smooth the data more aggressively, making local bumps disappear altogether.

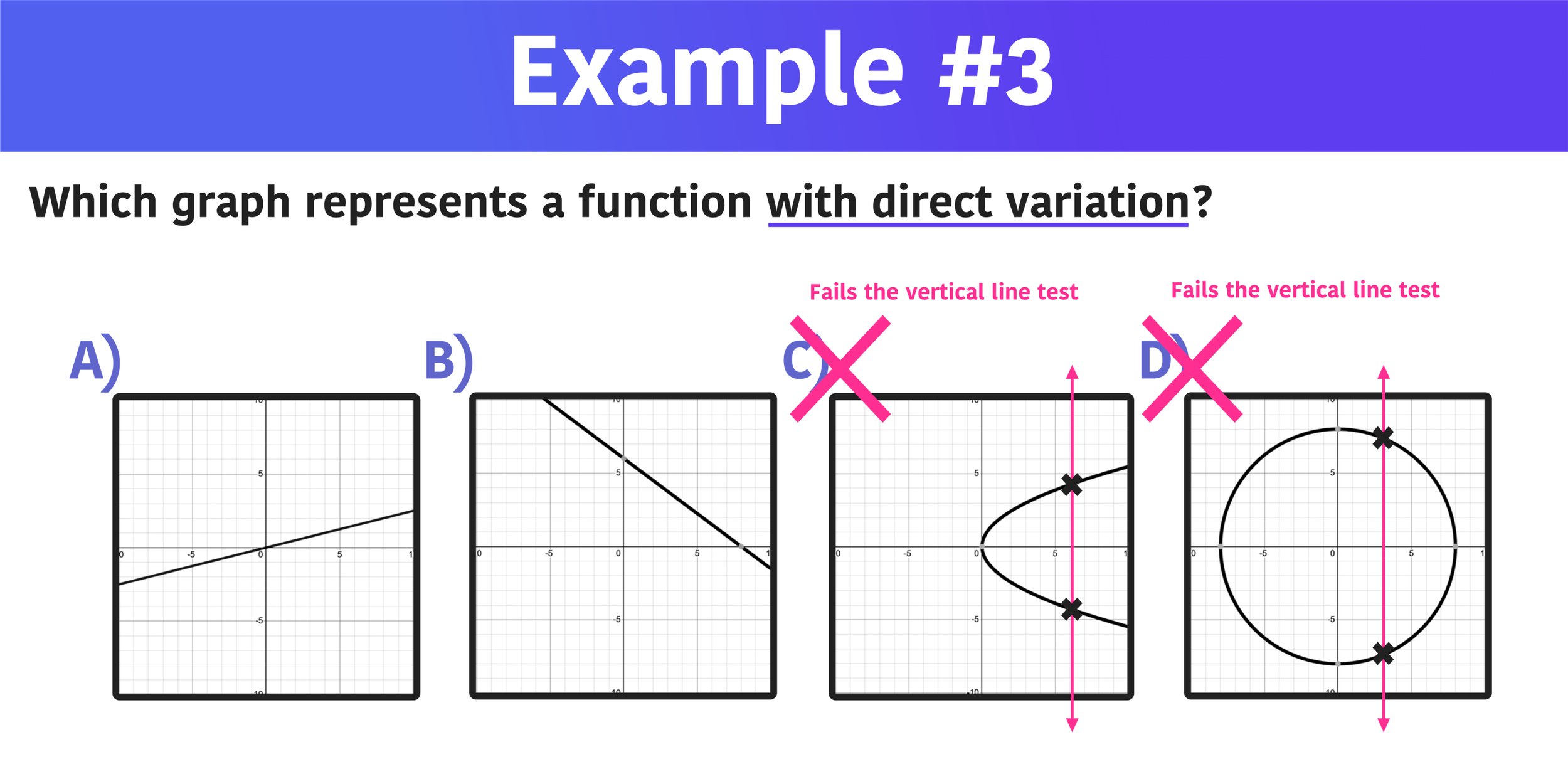
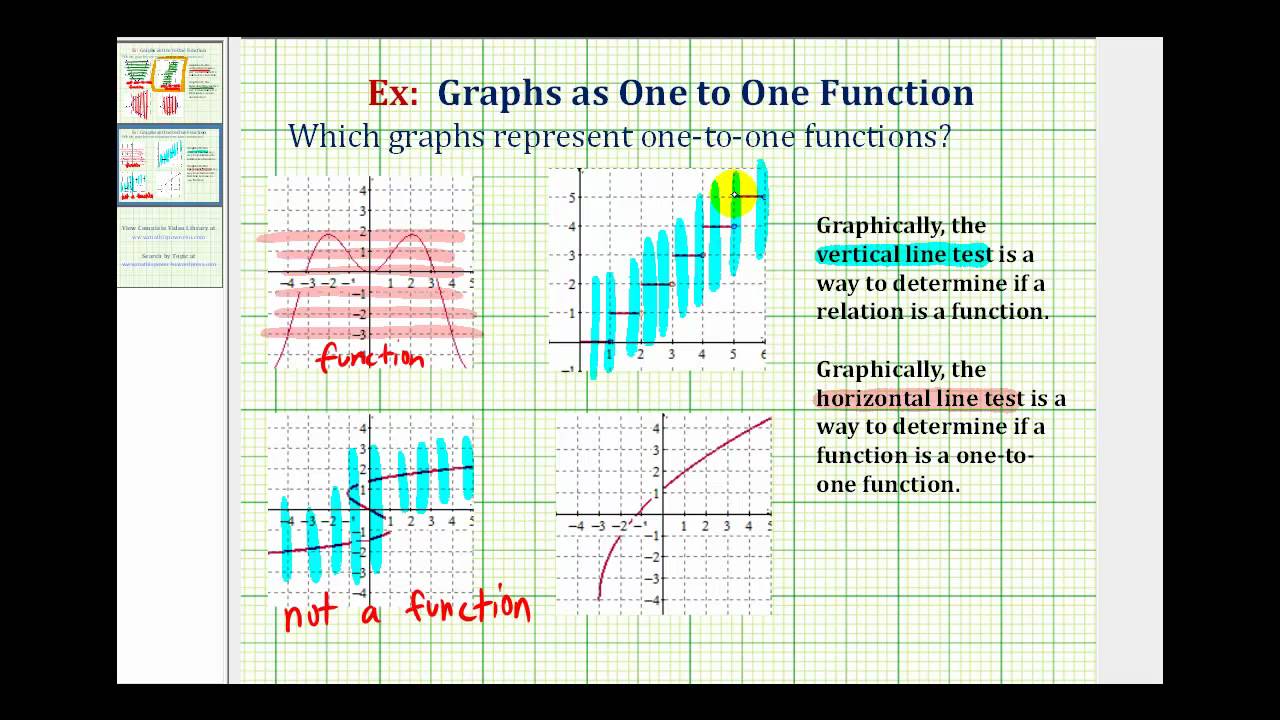
Use the sign analysis to determine whether f f is increasing or decreasing over that interval. Find the intercepts and use the multiplicities of the zeros to. Use the vertical line test to determine if the graph is the graph of a function.

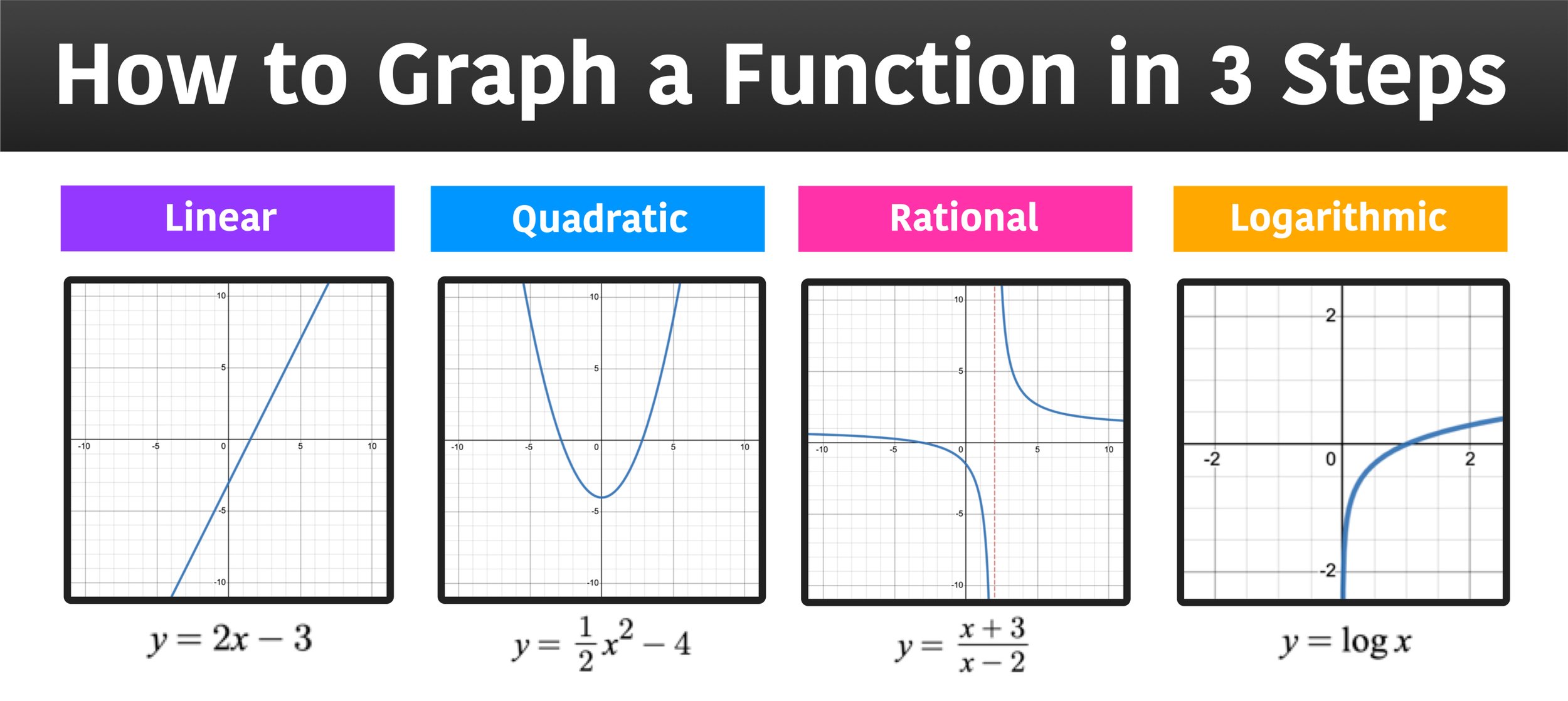
Determine the end behavior by examining the leading term. To see this tuning in effect, let's create a little test function to plot the results:. Given a polynomial function, sketch the graph.

In this video, i show that a curve described by a vector function is not smooth by showing there are values of t that make the derivative equal to zero. The algorithm for identifying whether or not a parametric curve is smooth contains a first step of finding out when dx/dt and dy/dt is simultaneously 0. In fact, for $x\rightarrow0^{\pm}$, $f(x)\sim \pm x$.

Explore math with our beautiful, free online graphing calculator. I have to determine whether the following curves are smooth or not and i'm having trouble with the following two functions: Reading the graph for function values we know that the graph of f pictured in figure.

Thanks to all of you who. Graphically, a smooth function of a single variable can be plotted as a single. Consider the following curve in the plane, $(x(t),y(t))$, this curve is called smooth if the functions $x(t)$ and $y(t)$ are smooth, which simply means that for all $n$, the.

Graph smoothing, also known as smoothing away or smoothing out, is the process of replacing edges e^'=v_iv_j and e^('')=v_jv_k incident at a vertex v_j of vertex. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Use first derivative test and the results of step 2 2 to determine whether f f has a local.

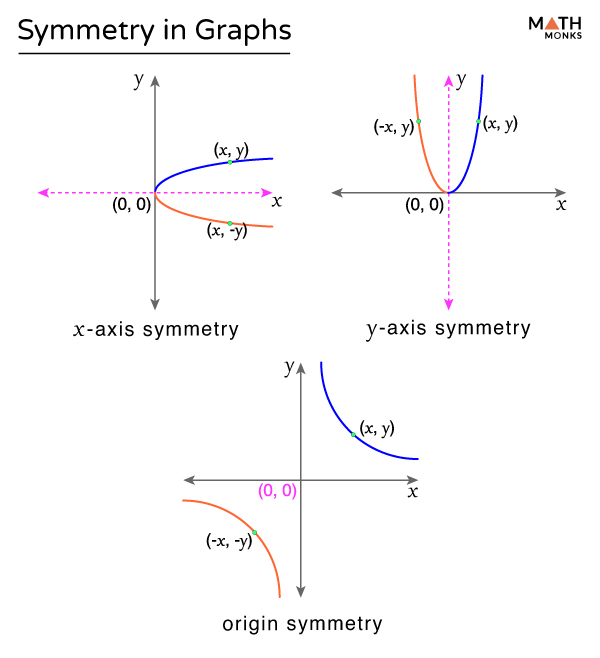
A graph for a function that's smooth without any holes, jumps, or asymptotes is called continuous. Inspect the graph to see if any vertical line drawn would intersect the curve. The right and left derivates in $x=0$ are $+1$.